
2.解:(Ⅰ)由题意及正弦定理,得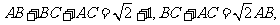
两式相减,得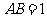 ,
,
(Ⅱ)由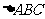 的面积
的面积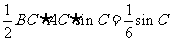 ,得
,得 ,
,
由余弦定理,得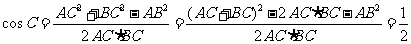 ,
,
所以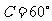 .
.
2.已知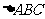 的周长为
的周长为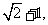 且
且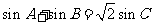 .
.
(Ⅰ)求边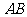 的长;
的长;
(Ⅱ)若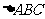 的面积为
的面积为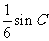 ,求角
,求角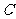 的度数.
的度数.
1.解:原方程变形为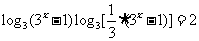 ,
,
即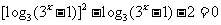 ,
,
设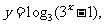 原方程可化为:
原方程可化为: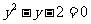 ,
,
解得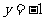 或
或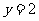 ,
,
即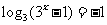 ,或
,或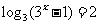 ,
,
于是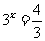 ,或
,或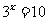 ,解得
,解得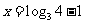 或
或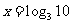
经检验他们都是原方程的解,
所以原方程的解集为 .
.
1.求解方程: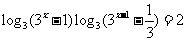 .
.
8.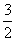 设球的半径长为
设球的半径长为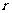 ,则
,则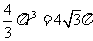 ,得
,得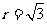 ,
,
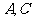 两点的球面距离
两点的球面距离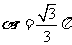 ,即
,即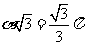 ,得
,得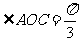 ,
,
即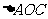 为等边三角形,得
为等边三角形,得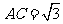 ,而
,而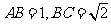 ,
,
得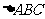 为直角三角形,且
为直角三角形,且 为斜边,而
为斜边,而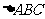 的外接圆的圆心在斜边
的外接圆的圆心在斜边 的中点上,
的中点上,
球心到平面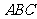 的距离为
的距离为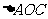 的边
的边 上的高,即
上的高,即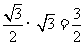 .
.
8.在体积为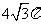 的球的表面上有
的球的表面上有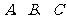 三点,
三点,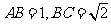 ,
,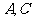 两点的
两点的
球面距离为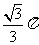 ,则球心到平面
,则球心到平面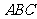 的距离为
.
的距离为
.
7.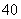 设六位数ABCDEF,先来讨论12排列的时候有多少,
设12对应AB,则CDEF有2×2×1×1=4;12对应BC,则ADEF有2×2×1×!=4;
12对应CD,则ABEF有2×2×1×1=4;12对应DE,则ABCF有2×2×1×1=4;
设六位数ABCDEF,先来讨论12排列的时候有多少,
设12对应AB,则CDEF有2×2×1×1=4;12对应BC,则ADEF有2×2×1×!=4;
12对应CD,则ABEF有2×2×1×1=4;12对应DE,则ABCF有2×2×1×1=4;
12对应EF,则ABCD有2×2×1×1=4,总共有4×5=20, 再讨论21排列的时候,这就不用算了, 肯定也是20,综上一共40个.
7.用1、2、3、4、5、6组成六位数(没有重复数字),要求任何相邻两个数的奇偶性不同,
且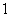 和
和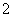 相邻,这样的六位数的个数是
.(用数字作答)
相邻,这样的六位数的个数是
.(用数字作答)
6.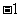 抛物线
抛物线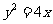 的焦点为
的焦点为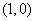 ,则
,则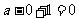 ,得
,得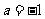 .
.
6.若直线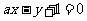 经过抛物线
经过抛物线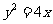 的焦点,则实数
的焦点,则实数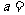 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com