
1、 ; 2、
; 2、 ; 3、
; 3、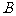 ;
;
2.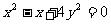 ; 3.
; 3.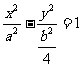 (提示:设
(提示:设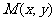 ,则
,则 将
将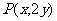 代入双曲线方程得
代入双曲线方程得 。); 4.
。); 4.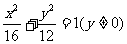 (提示:
(提示: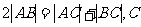 到AB的距离之和为8。)
到AB的距离之和为8。)
[例题探究]
例1.解析设P点的坐标为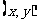 ,则由方程
,则由方程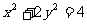 得
得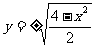 ,
,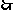 A、B两点的坐标分别为
A、B两点的坐标分别为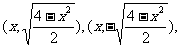 又
又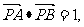
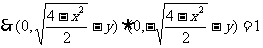 即
即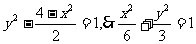 ,又直线
,又直线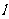 与椭圆交于两点,所以
与椭圆交于两点,所以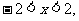 所以点P的轨迹方程为
所以点P的轨迹方程为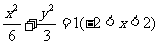 。
。
例2.解析(1)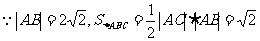 ,
,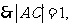 又
又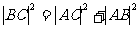 ,从而
,从而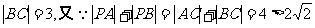 ,所以
,所以
点在以A、B为焦点,长半轴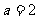 ,半焦距
,半焦距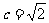 ,短半轴
,短半轴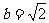 的椭圆
的椭圆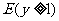 上,
上,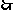 曲线E的方程为
曲线E的方程为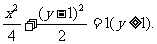
(2)设直线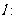
 ,代入E的方程,消
,代入E的方程,消 ,可得
,可得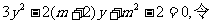
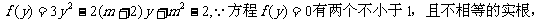 所以有
所以有 解之得
解之得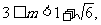 设
设 的中点为
的中点为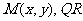 两点的坐标分别为
两点的坐标分别为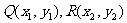 ,
,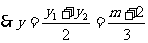
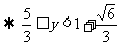 ,将
,将 得
得 所以
所以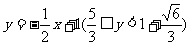 即为M点的轨迹方程。
即为M点的轨迹方程。
例3.解析(1)由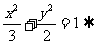 右准线
右准线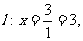 设
设 则由
则由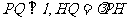 ,得
,得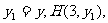 且
且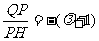 ,
,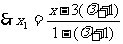 =
=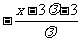 ,故有
,故有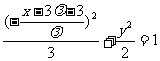 ,即
,即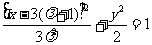 为所求点
为所求点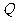 的轨迹G的方程。
的轨迹G的方程。
(2)当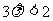 ,即
,即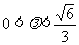 时,轨迹G是焦点在平行于
时,轨迹G是焦点在平行于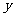 轴的直线上的椭圆,设其焦点
轴的直线上的椭圆,设其焦点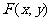 ,则
,则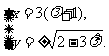 消去
消去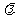 得
得
(3)当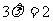 ,即
,即 时,轨迹G为圆,其方程为:
时,轨迹G为圆,其方程为: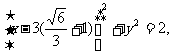 即
即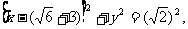 又
又
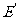 的右准线
的右准线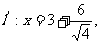 即
即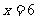
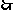 圆心G到准线
圆心G到准线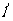 的距离为
的距离为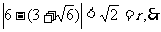 此时G与
此时G与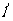 相交。
相交。
例4.解析:(1)直线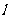 过点
过点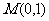 ,当斜率存在时,设其斜率为
,当斜率存在时,设其斜率为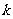 ,则
,则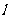 的方程为
的方程为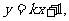 记
记 由题设可得点A、B的坐标
由题设可得点A、B的坐标 是方程组
是方程组 的解,消去
的解,消去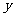 得
得
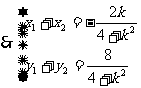 于是
于是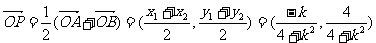 ,设点P的坐标为
,设点P的坐标为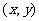 ,则
,则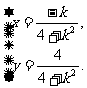 消去参数
消去参数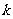 得
得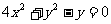 ①当
①当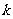 不存在时,A、B中点为坐标原点(0,0),也满足方程①,所以点P的轨迹方程为
不存在时,A、B中点为坐标原点(0,0),也满足方程①,所以点P的轨迹方程为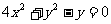 。
。
(1)
由点P的轨迹方程知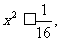 即
即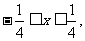
又 故
故
当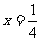 时,
时,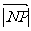 取得最小值为
取得最小值为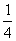 ;
;
当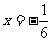 时,
时,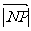 取得最大值为
取得最大值为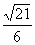 。
。
[冲刺强化训练18]
1.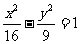 (提示:设动点
(提示:设动点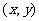 ,则
,则
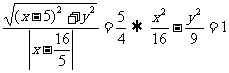 。);
。);
9.(1) 圆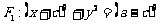 ,设
,设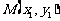 ,
,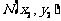 ,
,
则切线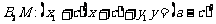 ,
,
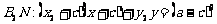 都过点
都过点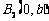 ,
,
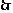
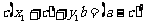 ;
;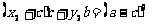
因此直线方程 就是过点
就是过点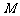 、
、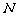 的直线。
的直线。
又直线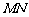 过点
过点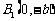 ,代入解方程可得:
,代入解方程可得:  ,
,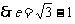
(2)直线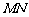 斜率为
斜率为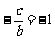 ,
,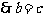 ,
,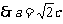 ,原点到直线
,原点到直线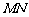 的距离为
的距离为
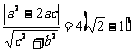 即
即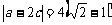 ,解得
,解得
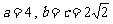 ,所求椭圆方程为:
,所求椭圆方程为: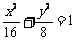
(3)由题意若存在,则有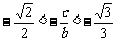 ,即
,即  ,得
,得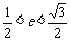
第18讲 求轨迹方程
[课前热身]
8.解:(1)由题设,直线AB的方程为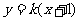 ,由
,由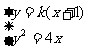 ,得
,得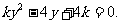 设
设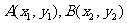 , 则
, 则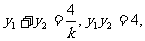
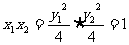 ,
,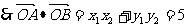 为常数。
为常数。
(2)设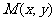 ,由
,由
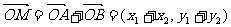 得
得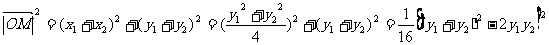
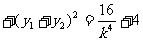 ,由于
,由于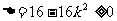 ,得
,得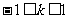 ,且
,且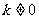 ,
,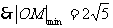 。
。
7.解:由条件知,双曲线焦点在 轴上,抛物线开口向右,所以抛物线方程为
轴上,抛物线开口向右,所以抛物线方程为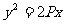
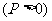 ,因为
,因为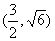 在抛物线上,所以
在抛物线上,所以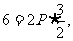 所以P=2,所以抛物线方程为
所以P=2,所以抛物线方程为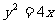 。因为抛物线的准线过双曲线的焦点,所以
。因为抛物线的准线过双曲线的焦点,所以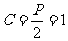 ,即
,即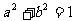 ①,又双曲线过点
①,又双曲线过点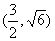 所以
所以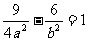 ②,由①②得
②,由①②得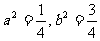 故双曲线方程为
故双曲线方程为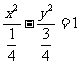
1.C 2、A 3、D 4、C 5.1 6.最大值6、最小值2
4.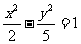
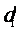
|

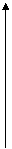 5.
5.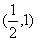 (提示:由定义得
(提示:由定义得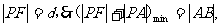 此时
此时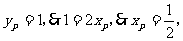 得
得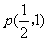 。)如图所示:
。)如图所示:
[例题探究]


 例1.[略解]:解析如图所示:
例1.[略解]:解析如图所示:




|
|


|


|

|

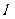 设
设 为左焦点,连结
为左焦点,连结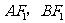 则根据椭圆的定义有:
则根据椭圆的定义有:
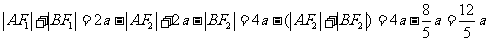
再设A、B、N三点到左准线的距离分别为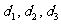 由梯形中位线定理,有
由梯形中位线定理,有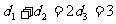 ,而已知
,而已知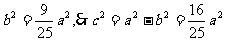 ,
,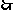 得离心率
得离心率
 ,
,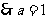 则椭圆方程为
则椭圆方程为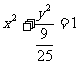
例2.[略解]:解析(1)右准线为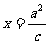 ,由对称性不妨设渐近线
,由对称性不妨设渐近线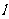 为
为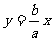 ,则
,则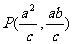 ,又
,又 ,又
,又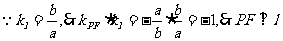
(2)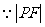 的长即
的长即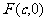 到
到 的距离,
的距离,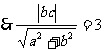 即
即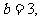 又
又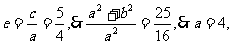 故双曲线的方程为
故双曲线的方程为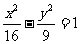
(3)PF的方程为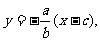 又
又 左准线
左准线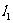 为
为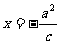
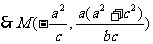
又 M是PN的中点,
M是PN的中点,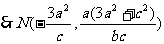 ,
, N在双曲线上,
N在双曲线上,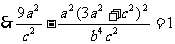 即
即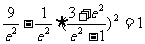 ,解得
,解得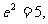 即
即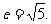
例3.解析(1)由抛物线的光学性质知光线PQ必经过抛物线的焦点F(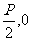 )
)
当直线PQ的倾斜角不为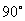 时,设 PQ的方程为
时,设 PQ的方程为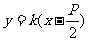 ,①
,①
由①式得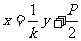 ,将其代入抛物线方程
,将其代入抛物线方程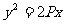 中,整理得
中,整理得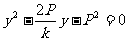
由韦达定理得 .
.
当直线PQ的倾斜角为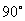 时,将
时,将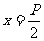 代入抛物线方程,得
代入抛物线方程,得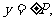 同样可以得到
同样可以得到
(2)因为光线QN经直线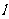 反射后又射向M点,所以MN与QN关于直线
反射后又射向M点,所以MN与QN关于直线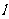 反射对称,设点M(
反射对称,设点M(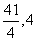 )关于
)关于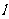 的对称点为
的对称点为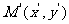 ,则
,则
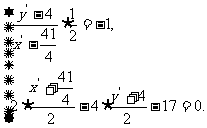 解得
解得 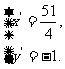
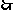 直线QN的方程为
直线QN的方程为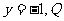 点纵坐标
点纵坐标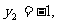 又
又 由题设知P点的纵坐标
由题设知P点的纵坐标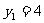 ,且由(1)知
,且由(1)知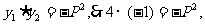 得P=2,所以抛物线的方程为
得P=2,所以抛物线的方程为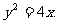
(3)将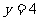 代入
代入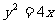 ,得
,得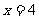 ,故P点坐标为(
,故P点坐标为(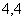 );
);
将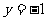 代入直线
代入直线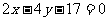 ,得
,得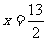 ,故N点坐标为(
,故N点坐标为( )
)
由N、P两点坐标得直线PN的方程为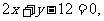 设M点关于直线PN的对称点
设M点关于直线PN的对称点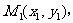 则
则

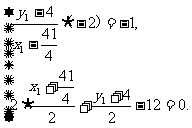 解得
解得 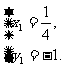
将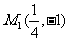 代入抛物线方程
代入抛物线方程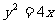 ,原式成立。故抛物线上存在一点
,原式成立。故抛物线上存在一点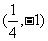 与点M关于直线PN对称。
与点M关于直线PN对称。
[强化训练17]
2.C 3.B(提示: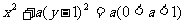 ,即
,即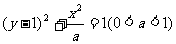 ,椭圆的下顶点与O点重合,则OP长度的最大值即为长轴的长。)
,椭圆的下顶点与O点重合,则OP长度的最大值即为长轴的长。)
1.D(提示:①当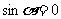 时,
时,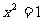 ,曲线为两条平行于
,曲线为两条平行于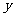 轴的直线;②当
轴的直线;②当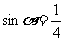 时,
时,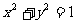 ,曲线为圆;③当
,曲线为圆;③当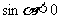 时,曲线为双曲线;④当
时,曲线为双曲线;④当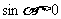 且
且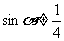 时,曲线为椭圆,故不可能为抛物线。)
时,曲线为椭圆,故不可能为抛物线。)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com