
10. (06年江苏卷)已知三点P(5,2)、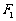 (-6,0)、
(-6,0)、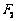 (6,0). (☆P21 例4)
(6,0). (☆P21 例4)
(1)求以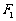 、
、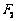 为焦点且过点P的椭圆的标准方程;(2)设点P、
为焦点且过点P的椭圆的标准方程;(2)设点P、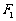 、
、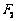 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为 、
、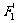 、
、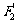 ,求以
,求以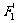 、
、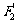 为焦点且过点
为焦点且过点 的双曲线的标准方程。
的双曲线的标准方程。
解:(1)设所求椭圆方程为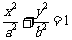 (a>b>0),其半焦距c=6,……(2分)
(a>b>0),其半焦距c=6,……(2分)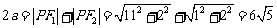 ……(4分)
……(4分)
∴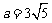 ,b2=a2-c2=9. 所以所求椭圆的标准方程为
,b2=a2-c2=9. 所以所求椭圆的标准方程为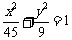 . ……(6分)
. ……(6分)
(2)点P(5,2)、F1(-6,0)、F2(6,0)关于直线y=x的对称点分别为点P,(2,5)、F1,(0,-6)、F2,(0,6). ……(8分)
设所求双曲线的标准方程为 ,由题意知,半焦距c1=6,
,由题意知,半焦距c1=6,
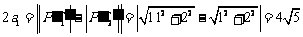 ,
,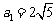 ,b12=c12-a12=36-20=16.
,b12=c12-a12=36-20=16.
所以,所求双曲线的标准方程为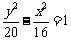 .……(12分)
.……(12分)
9.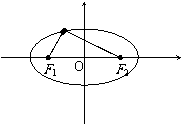 点M是椭圆
点M是椭圆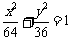 上的一点,F1、F2是左右焦点,∠F1MF2=60º,求△F1MF2的面积.
上的一点,F1、F2是左右焦点,∠F1MF2=60º,求△F1MF2的面积.
解:由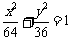 ,得a=8,b=6,
,得a=8,b=6,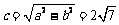 .……(3分)
.……(3分)
根据椭圆定义,有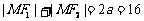 .……(5分)
.……(5分)
在△F1MF2中,由余弦定理,得到
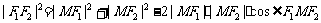 .
.
即 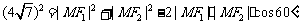 ,……(7分)
,……(7分)
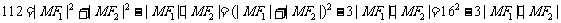 ,
,
解得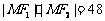 .……(10分)
.……(10分)
△F1MF2的面积为: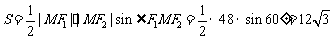 .……(12分)
.……(12分)
8. 在抛物线 上求一点P,使得点P到直线
上求一点P,使得点P到直线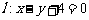 的距离最短, 并求最短距离.
的距离最短, 并求最短距离.
解:设与直线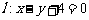 平行,且与抛物线
平行,且与抛物线 相切的直线为
相切的直线为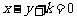 .……(3分)
.……(3分)
由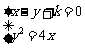 , 消x得
, 消x得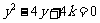 .……(5分)
.……(5分)
∴  ,解得
,解得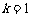 ,即切线为
,即切线为 .……(7分)
.……(7分)
由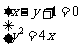 ,解得点
,解得点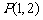 . ……(9分)
. ……(9分)
∴ 最短距离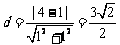 .……(12分)
.……(12分)
7. 已知椭圆C的焦点分别为F1(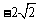 ,0)和F2(2
,0)和F2(2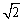 ,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点. 求:(1)线段AB的中点坐标; (2)弦AB的长.
,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点. 求:(1)线段AB的中点坐标; (2)弦AB的长.
解:设椭圆C的方程为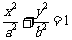 ,由题意a=3,c=2
,由题意a=3,c=2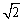 ,于是b=
,于是b=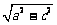 =1. ……(3分)
=1. ……(3分)
∴ 椭圆C的方程为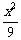 +y2=1.……(5分)
+y2=1.……(5分)
联立方程组 ,消y得10x2+36x+27=0,
,消y得10x2+36x+27=0,
因为该二次方程的判别式Δ>0,所以直线与椭圆有两个不同的交点,……(9分)
设A(x1,y1),B(x2,y2),则x1+x2=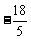 ,故线段AB的中点坐标为(
,故线段AB的中点坐标为(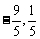 ).……(12分)
).……(12分)
6. 一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.
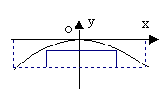 (1)建立如图所示的平面直角坐标系xoy,试求拱桥所在抛物线的方程;
(1)建立如图所示的平面直角坐标系xoy,试求拱桥所在抛物线的方程;
(2)若一竹排上有一4米宽6米高的大木箱,问此木排能否安全通过此桥?
解:(1)设抛物线方程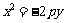 .……(2分)
.……(2分)
由题意可知,抛物线过点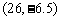 ,代入抛物线方程,得
,代入抛物线方程,得
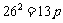 , 解得
, 解得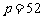 ,
,
所以抛物线方程为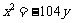 . ……(6分)
. ……(6分)
(2)把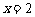 代入,求得
代入,求得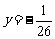 . ……(9分)
. ……(9分)
而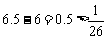 ,所以木排能安全通过此桥. ……(12分)
,所以木排能安全通过此桥. ……(12分)
5. 当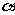 从
从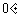 到
到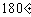 变化时,方程
变化时,方程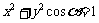 表示的曲线的形状怎样变换?
表示的曲线的形状怎样变换?
解:当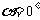 时,
时,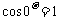 ,方程
,方程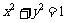 表示圆心在原点的单位圆。……(3分)
表示圆心在原点的单位圆。……(3分)
当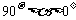 时,
时,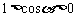 ,方程
,方程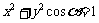 表示圆心在原点的单位圆。……(5分)
表示圆心在原点的单位圆。……(5分)
当 时,
时,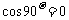 ,方程
,方程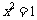 ,得
,得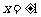 表示与
表示与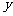 轴平行的两条直线。……(7分)
轴平行的两条直线。……(7分)
当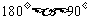 时,
时,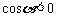 ,方程
,方程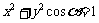 表示焦点在
表示焦点在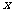 轴上的双曲线。……(9分)
轴上的双曲线。……(9分)
当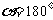 时,
时,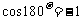 ,方程
,方程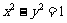 表示焦点在
表示焦点在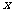 轴上的等轴双曲线。……(12分)
轴上的等轴双曲线。……(12分)
4. 倾斜角为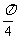 的直线l经过抛物线
的直线l经过抛物线 的焦点,且与抛物线相交于A、B两点,求线段AB的长. (◎P61 例4)
的焦点,且与抛物线相交于A、B两点,求线段AB的长. (◎P61 例4)
解:设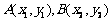 ,
,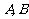 到准线的距离分别为
到准线的距离分别为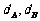 ,
,
由抛物线的定义可知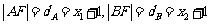 ,于是
,于是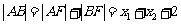 。……(3分)
。……(3分)
由已知得抛物线的焦点为 ,斜率
,斜率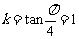 ,所以直线
,所以直线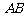 方程为
方程为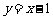 。……(6分)
。……(6分)
将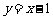 代入方程
代入方程 ,得
,得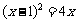 ,化简得
,化简得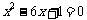 。由求根公式得
。由求根公式得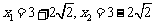 ,……(9分)
,……(9分)
于是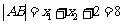 。所以,线段AB的长是8。……(12分)
。所以,线段AB的长是8。……(12分)
3. 双曲线的离心率等于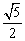 ,且与椭圆
,且与椭圆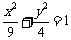 有公共焦点,求此双曲线的方程. (◎P68 4)
有公共焦点,求此双曲线的方程. (◎P68 4)
解:椭圆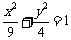 焦点为
焦点为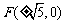 ,根据题意得双曲线的焦点为
,根据题意得双曲线的焦点为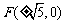 ,……(3分)
,……(3分)
设双曲线的标准方程为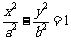 ,且有
,且有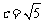 。……(6分)
。……(6分)
又由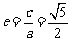 ,得
,得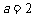 ,得
,得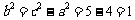 ,……(10分)
,……(10分)
所求双曲线的方程为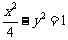 。……(2分)
。……(2分)
2. 点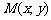 与定点
与定点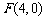 的距离和它到直线
的距离和它到直线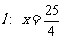 的距离的比是常数
的距离的比是常数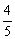 ,求M的轨迹.(◎P41 例6)
,求M的轨迹.(◎P41 例6)
解:设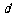 是点
是点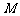 到直线
到直线 的距离,根据题意得,点
的距离,根据题意得,点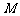 的轨迹就是集合
的轨迹就是集合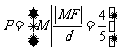 ,……(4分)
,……(4分)
由此得 。将上式两边平方,并化简,得
。将上式两边平方,并化简,得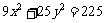 。即
。即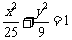 。……(9分)
。……(9分)
所以,点M的轨迹是长轴、短轴长分别为10、6的椭圆。. ……(12分)
1. 已知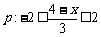 ,
,  , 若
, 若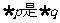 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围. (☆P6 9)
的取值范围. (☆P6 9)
解:∵﹁p 是﹁q必要不充分条件, ∴ 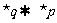 ,即
,即 .……(3分)
.……(3分)
解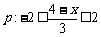 得
得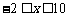 ,即:
,即: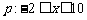 . ……(6分)
. ……(6分)
解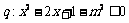 变形为
变形为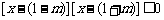 ,解得
,解得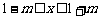 ,
,
即 .
……(9分)
.
……(9分)
由 ,则
,则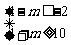 ,解得
,解得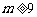 .
.
所以实数 的取值范围
的取值范围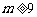 。
……(12分)
。
……(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com