
4. (同上)考点:合情推理及证明
(1)若三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积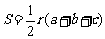 ,根据类比思想,若四面体的内切球半径为R,四个面的面积分别为
,根据类比思想,若四面体的内切球半径为R,四个面的面积分别为 ,则此四面体的体积V= .
,则此四面体的体积V= .
(2)(2003年全国卷)在平面几何里有勾股定理:“设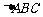 的两边
的两边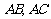 互相垂直,则
互相垂直,则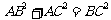 .” 拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积之间的关系,可以得出的正确结论是:“设三棱锥
.” 拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积之间的关系,可以得出的正确结论是:“设三棱锥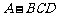 的三侧面
的三侧面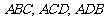 两两垂直,则
.”
两两垂直,则
.”
 解:(1)设四面体内切球的球心为O,则球心O到四个面
解:(1)设四面体内切球的球心为O,则球心O到四个面 的距离都是R,所以四面体的体积等于以O为顶点,分别以
的距离都是R,所以四面体的体积等于以O为顶点,分别以 为底面的四个三棱锥体积的和.
为底面的四个三棱锥体积的和.
所以,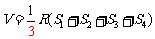 .
.
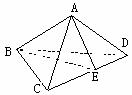
(2)线的关系类比到面的关系,猜测: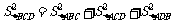 . 证明如下:
. 证明如下:
如图作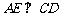 连
连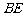 ,则
,则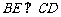 .
.
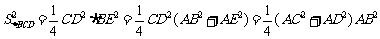
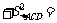
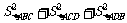
3. 考点:合情推理及证明
已知 ,分别求
,分别求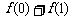 ,
,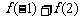 ,
,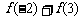 ,然后归纳猜想一般性结论,并证明你的结论.
,然后归纳猜想一般性结论,并证明你的结论.
解:由 ,得
,得
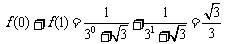 ;
;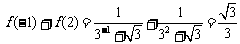 ;
;
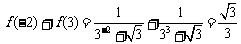 .
.
归纳猜想一般性结论为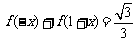 .
.
证明如下:
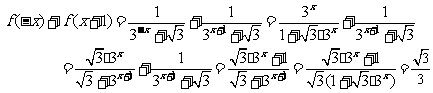
2. 考点:①会根据数据绘制 列连表②能利用公式判断两个量之间的相关性(独立性检验)
列连表②能利用公式判断两个量之间的相关性(独立性检验)
甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)试判断是否成绩与班级是否有关? (◎P17 练习改编)
参考公式: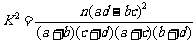 ;
;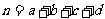
|
P(K2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
解:(1)2×2列联表如下:
|
|
不及格 |
及格 |
总计 |
|
甲班 |
4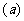 |
36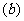 |
40 |
|
乙班 |
16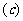 |
24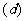 |
40 |
|
总计 |
20 |
60 |
80 |
(2)
由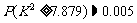 ,所以有99.5%的把握认为“成绩与班级有关系”.
,所以有99.5%的把握认为“成绩与班级有关系”.
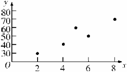
1. 考点:①会画散点图②能利用公式求线性回归方程
某种产品的广告费用支出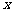 (万元)与销售额
(万元)与销售额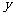 (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
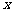 |
2 |
4 |
5 |
6 |
8 |
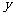 |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入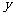 的值.
的值.
参考公式:回归直线的方程 ,其中
,其中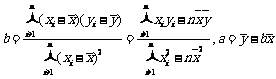 .
.
解:(1)作出散点图如下图所示:
(2)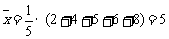 ,
,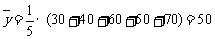 ,
,
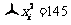 ,
, ,
,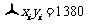 .
.
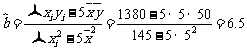 ,
,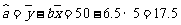 .
.
因此回归直线方程为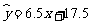 ;
;
(3)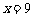 时,预报
时,预报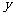 的值为
的值为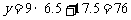 (万元).
(万元).
16.(2006年江西卷)已知函数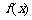
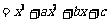 在
在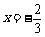 与
与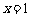 时都取得极值,(☆P49 例2)
时都取得极值,(☆P49 例2)
(1)求a、b的值与函数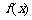 的单调区间.
的单调区间.
(2)若对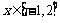 时,不等式
时,不等式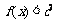 恒成立,求c的取值范围.
恒成立,求c的取值范围.
解:(1)
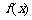
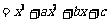 ,
,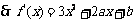 .……(3分)
.……(3分)
由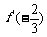
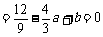 ,
,
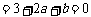 得a=
得a=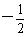 ,b=-2
,b=-2

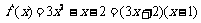 ,
,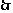 当x变化时,
当x变化时,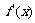 、
、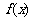 的变化情况如下表:
的变化情况如下表:
|
x |
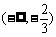 |
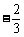 |
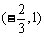 |
1 |
 |
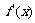 |
+ |
0 |
- |
0 |
+ |
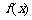 |
|
极大值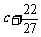 |
 |
极小值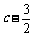 |
|
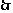 函数
函数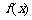 的递增区间是(-¥,-
的递增区间是(-¥,-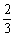 )和(1,+¥);递减区间是(-
)和(1,+¥);递减区间是(-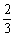 ,1). ……(6分)
,1). ……(6分)
(2)
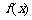 =x3-
=x3-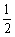 x2-2x+c
x2-2x+c 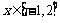 ,……(8分)
,……(8分)
又
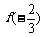 =
=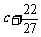 ,
,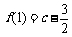 ,
,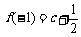 ,
,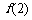 =c+2.
=c+2.
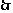
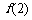 =c+2为最大值. ……(10分)
=c+2为最大值. ……(10分)
要使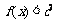 在
在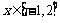 恒成立,只需
恒成立,只需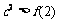 =c+2,解得c<-1或c>2. ……(12分)
=c+2,解得c<-1或c>2. ……(12分)
答案整理:贺联梅
欢迎将错误反馈到zssxzb@
15. ( 2005年全国卷III.文)用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少? (☆P47 例1)
 解:设容器的高为x,容器的体积为V,……(1分)
解:设容器的高为x,容器的体积为V,……(1分)
则V=(90-2x)(48-2x)x,(0<x<24)……(5分)
=4x3-276x2+4320x
∵V′=12 x2-552x+4320
令V′=12 x2-552x+4320=0得x1=10,x2=36. ……(8分)
∵令V′>0得x>36或x<10 ;令V′<0得10<x<36.
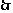 函数在
函数在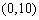 上递增,在
上递增,在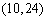 上递减.
上递减. 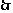 当x=10时,V有极大值
当x=10时,V有极大值 =19600.
=19600.
又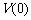 =0,
=0,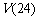 =0, 所以当x=10时,V有最大值
=0, 所以当x=10时,V有最大值 =19600cm
=19600cm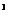 .……(12分)
.……(12分)
14. 已知a为实数,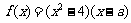 ,(1)求导数
,(1)求导数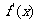 ;
;
(2)若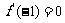 ,求
,求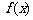 在
在 上的最大值和最小值;
上的最大值和最小值;
(3)若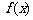 在
在 和
和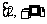 上都是增函数,求a的取值范围. (☆P45 例3)
上都是增函数,求a的取值范围. (☆P45 例3)
解:(1)因为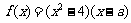 =
=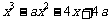 ,所以
,所以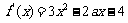 .……(3分)
.……(3分)
(2)由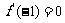 ,得
,得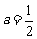 , 此时有
, 此时有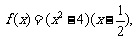 所以
所以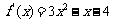 ……(5分)
……(5分)
由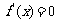 ,得
,得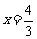 或
或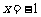 ,又因为
,又因为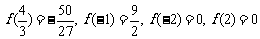 ,
,
所以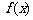 在
在 上的最大值为
上的最大值为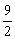 ,最小值为
,最小值为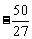 .……(8分)
.……(8分)
(3)
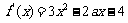 的图象为开口向上且过点(0,-4)的抛物线.
的图象为开口向上且过点(0,-4)的抛物线.
由条件得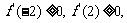 即
即 ,解得
,解得 . 所以
. 所以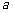 的取值范围为
的取值范围为 .……(12分)
.……(12分)
13.(06年福建卷)已知函数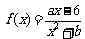 的图象在点
的图象在点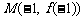 处的切线方程为
处的切线方程为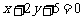 .
.
(1)求函数 的解析式;(2)求函数
的解析式;(2)求函数 的单调区间.
(☆P50 8)
的单调区间.
(☆P50 8)
解:(1)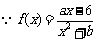 ,
,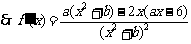 .……(2分)
.……(2分)
又 函数
函数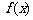 的图象在点
的图象在点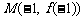 处的切线方程为x+2y+5=0, ……(4分)
处的切线方程为x+2y+5=0, ……(4分)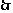
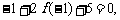
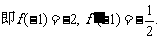
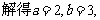
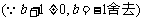
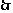 所求函数解析式为
所求函数解析式为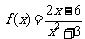 .……(6分)
.……(6分)
(2)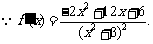
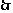
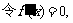 解得
解得 ……(8分)
……(8分)
当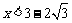 或
或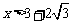 时,
时,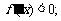 当
当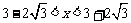 时,
时,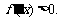
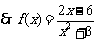 在
在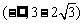 和
和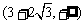 内是减函数,在
内是减函数,在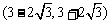 内是增函数. ……(12分)
内是增函数. ……(12分)
12. 设函数 .
.
(1)求函数f(x)的单调区间;
(2)求函数f(x)的极大值和极小值.
解:∵ f′(x)=-x2+4x-3=-(x-3)(x-1), ……(2分)
(1)由f′(x)>0,解得:1<x<3;由f′(x)<0,解得:x<1或x>3,
则函数f(x)的单调递增区间为(1, 3),单调递减区间为(-∞,1)和(3,+∞). ……(6分)
(2)由f′(x)=0,解得:x=1或x=3. 列表如下:……(9分)
|
x |
(-∞,1) |
1 |
(1,
3) |
3 |
(3,+ ∞) |
|
f′(x) |
- |
0 |
+ |
0 |
- |
|
f(x) |
单调递减↘ |
- |
单调递增↗ |
0 |
单调递减 ↘ |
∴函数f(x)的极大值为0,极小值为- .……(12分)
.……(12分)
11. 已知函数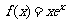 (
(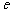 为自然对数的底).
为自然对数的底).
(1)求函数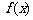 的单调递增区间;
的单调递增区间;
(2)求曲线 在点
在点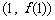 处的切线方程.
处的切线方程.
解: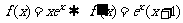 ,因此有……(3分)
,因此有……(3分)
(1)令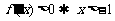 ,即函数
,即函数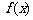 的单调递增区间是
的单调递增区间是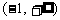 ;……(6分)
;……(6分)
(2)因为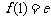 ,
, ,……(9分)
,……(9分)
所以曲线 在点
在点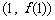 处的切线方程为
处的切线方程为
 ,即
,即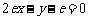 .……(12分)
.……(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com