
1. 试选择适当的方法表示下列集合:
(1)函数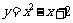 的函数值的集合; (2)
的函数值的集合; (2)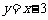 与
与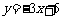 的图象的交点集合.
的图象的交点集合.
12. 考点:绝对值不等式(涉及分段函数的图像)
(2007年宁夏、海南.理)设函数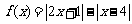 .
.
(1)解不等式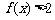 ;
;
(2)求函数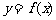 的最小值.
的最小值.
解:(1)令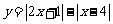 ,则
,则

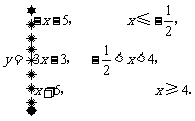
作出函数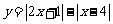 的图象,
的图象,
它与直线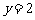 的交点为
的交点为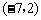 和
和 .
.
所以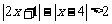 的解集为
的解集为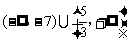 .
.
(2)由函数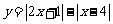 的图像可知,当
的图像可知,当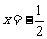 时,
时,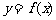 取得最小值
取得最小值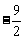 .
.
答案整理:赵进
欢迎将错误反馈到zssxzb@
11. 考点:数学归纳法(步骤)
数列 满足
满足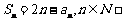 .(
.(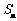 为前n项和)
为前n项和)
(1)计算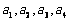 ,并由此猜想
,并由此猜想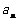 ;(2)用数学归纳法证明(1)中的结论.
;(2)用数学归纳法证明(1)中的结论.
解:(1)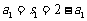 ,
,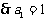 ,
,
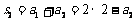 ,
,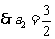 ,
, 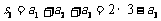 ,
,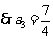 ,
,
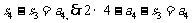 ,
,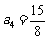 ,
,
猜想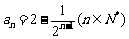 .
.
(2)证明:①当n=1时,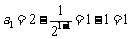 ,猜想结论成立.
,猜想结论成立.
②假设当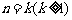 时结论成立,即
时结论成立,即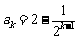 .
.
当n=k+1时 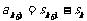 =2
=2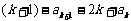 ,
,
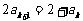 ,
, 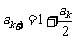 =
=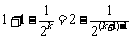 .
.
所以当n=k+1时,猜想结论成立.
由(1)和(2)可知,对一切 结论成立.
结论成立.
10. 考点:①求概率②求随机变量的分布列和期望
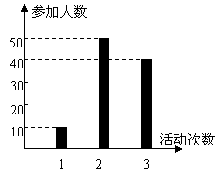
(07年北京高考.理18)某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(1)求合唱团学生参加活动的人均次数;
(2)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
 (3)从合唱团中任选两名学生,用
(3)从合唱团中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望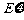 .
.
解:由图可知,参加活动1次、2次和3次的学生人数分别为10、 50和40.
(1)该合唱团学生参加活动的人均次数为
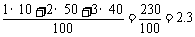 .
.
(2)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为  .
.
(3)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件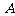 ,“这两人中一人参加2次活动,另一人参加3次活动”为事件
,“这两人中一人参加2次活动,另一人参加3次活动”为事件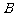 ,“这两人中一人参加1次活动,另一人参加3次活动”为事件
,“这两人中一人参加1次活动,另一人参加3次活动”为事件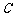 .易知
.易知
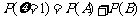
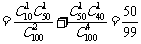 ;
;
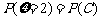
 ;
;
 的分布列:
的分布列:
 |
0 |
1 |
2 |
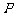 |
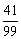 |
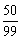 |
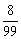 |
 的数学期望:
的数学期望: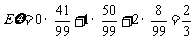 .
.
9. 考点:利用空间向量解决立体几何问题(涉及空间直角坐标系的建立、空间点坐标的表示、空间向量数量积的运算、平面向量定理、空间向量垂直的判定)
如图,PD垂直正方形ABCD所在平面,AB=2,E是PB的中点,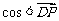 ,
,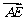 )
)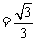 .
.
(1)建立适当的空间坐标系,写出点E的坐标;
(2)在平面PAD内求一点F,使EF⊥平面PCB.
解:(1)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,则
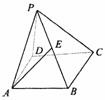 A(2,0,0),B(2,2,0),C(0,2,0).
A(2,0,0),B(2,2,0),C(0,2,0).
设P(0,0,2m),则E(1,1,m).
∴ 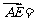 (-1,1,m),
(-1,1,m),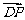 =(0,0,2m),
=(0,0,2m),
∴ 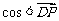 ,
, ,解得
,解得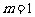 .
.
∴ 点E坐标是(1,1,1).
(2)∵ 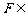 平面PAD, ∴ 可设F(x,0,z)
平面PAD, ∴ 可设F(x,0,z)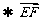 =(x-1,-1,z-1).
=(x-1,-1,z-1).
∵ EF⊥平面PCB ,∴ 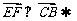
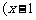 ,-1,
,-1,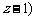
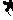 2,0,
2,0,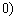
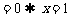 .
.
∵ 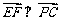 , ∴
, ∴ 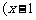 ,-1,
,-1,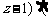 0,2,-2
0,2,-2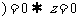 .
.
∴ 点F的坐标是(1,0,0),即点F是AD的中点.
另解:由平面向量定理,设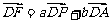 ,即
,即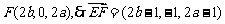
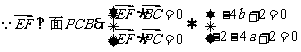
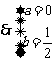 ,即
,即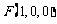
8. 考点:复数的几何意义(对应复平面上的点)
已知z是复数,z+2i、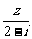 均为实数,且复数
均为实数,且复数 在复平面上对应的点在第一象限,求实数a的取值范围.
在复平面上对应的点在第一象限,求实数a的取值范围.
解:根据题意,设复数z=c+di,
则z+2i=c+(d+2)i为实数,即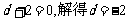 ,解得 所以
,解得 所以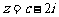 .
.
又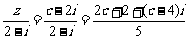 为实数,即
为实数,即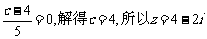 .
.
而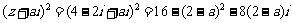 对应的点在第一象限,
对应的点在第一象限,
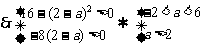 , 解得2<a<6.
, 解得2<a<6.
所以实数a的取值范围是2<a<6.
7.考点:①复数的运算②复数的共轭
(1)已知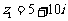 ,
,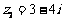 ,
, ,求z. (◎P65 3)
,求z. (◎P65 3)
(2)已知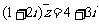 ,求z及
,求z及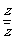 . (◎P65 B1)
. (◎P65 B1)
解:(1)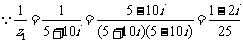 ,
,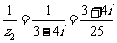
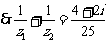 ,故
,故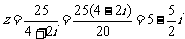
(2)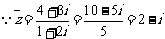
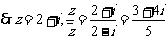
6. 证明:(1)∵ 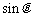 与
与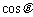 的等差中项是
的等差中项是 ,等比中项是
,等比中项是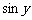 ,
,
∴ 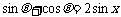 , ①
, ① 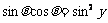 , ②
, ②
①2-②×2,可得 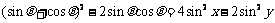 , 即
, 即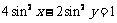 .
.
∴ 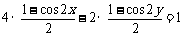 , 即
, 即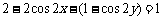 .故证得
.故证得 .
.
(2)要证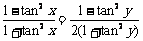 ,只需证
,只需证 ,
,
即证 ,即证
,即证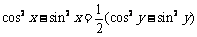 ,只需证
,只需证 .
.
由(1)的结论, 显然成立. 所以,
显然成立. 所以,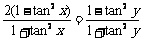 .
.
6.考点:证明方法的合理利用
已知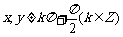 ,
,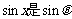 ,
,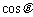 的等差中项,
的等差中项,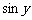 是
是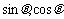 的等比中项.
的等比中项.
求证:(1) ; (2)
; (2)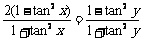 . (☆P18 9,◎P43 例6)
. (☆P18 9,◎P43 例6)
5. 考点:综合法、分析法、反证法的步骤和格式
试分别用综合法、分析法、反证法等三种方法,证明下列结论: 已知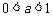 ,则
,则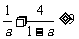 .
.
解:[分析法]: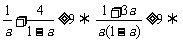
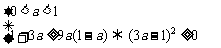
[反证法]:假设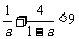 ,通分得
,通分得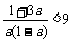 .
.
∵ 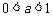 , ∴
, ∴ 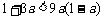 , 整理得
, 整理得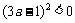 ,这与平方数不小于0矛盾.
,这与平方数不小于0矛盾.
∴ 假设不成立, 则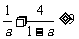 .
.
[综合法]:由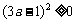 ,变形得
,变形得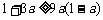 .
.
∵ 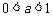 , ∴
, ∴ 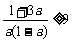 , 即
, 即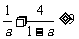 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com