1. 已知角a的终边经过P(4,-3).

(1)求2sina－cosa的值；　 (2)求角a的终边与单位圆的交点P的坐标.

8.(09年广东卷.文)随机抽取某中学甲乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图.

(1)根据茎叶图判断哪个班的平均身高较高；

(2)计算甲班的样本方差；

(3)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学，求身高为176 cm的同学被抽中的概率.

7.(08年广东卷.文)某初级中学共有学生2000名，各年级男、女生人数如下表：

已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.

(1)求x的值； (2)现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？

(3)已知y245, z245,求初三年级中女生比男生多的概率.

6. (2008年韶关模拟)某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩(均为整数)分成六段，…后画出如下部分频率分布直方图. 观察图形的信息，回答下列问题：

(1)求第四小组的频率，并补全这个频率分布直方图；

(3)估计这次考试的及格率(60分及以上为及格)和平均分；

(3)从成绩是80分以上(包括80分)的学生中选两人，求他们选在同一组的概率.

5. 在一次商贸交易会上，商家在柜台开展促销抽奖活动，甲、乙两人相约同一天上午去该柜台参与抽奖.

(1)若抽奖规则是从一个装有6个红球和4个白球的袋中无放回地取出2个球，当两个球同色时则中奖，求中奖概率；　 (2)若甲计划在9：00-9：40之间赶到，乙计划在9：20-10：00之间赶到，求甲比乙提前到达的概率.

4. 假设关于某设备的使用年限x和所支出的维修费用y(万元)，有如下的统计资料：　 (☆P₂₂ 8)

若由资料可知y对x呈线性相关关系，试求：

(1)回归直线方程；(2)估计使用年限为10年时，维修费用约是多少？(参考：)

3. 甲、乙两种玉米苗中各抽10株，分别测得它们的株高如下(单位：cm)：　 (☆P₁₇ 例3)

甲：25 41 40 37 22 14 19 39 21 42

乙：27 16 44 27 44 16 40 40 16 40

问：(1)哪种玉米的苗长得高？(2)哪种玉米的苗长得齐？

2. 对某电子元件进行寿命追踪调查，情况如下.　　　　　　　 (☆P₁₅ 例3)

(1)列出频率分布表；(2)画出频率分布直方图；(3)估计元件寿命在100-400 h以内的在总体中占的比例；(4)估计电子元件寿命在400 h以上的在总体中占的比例.

1. 设计一个算法求的值，并画出程序框图.　 (◎P₂₀ 2)

16. 求圆心在直线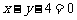上，并且经过圆与圆的交点的圆的方程. (◎P₁₃₂ 4)