17、(本小题满分12分)

　甲盒有标号分别为1、2、3的3个红球；乙盒有标号分别为1，2，…，n(n≥2)的n个黑球，从甲、乙两盒中各抽取一个小球，抽取的标号恰好分别为1和n的概率为．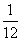

　(1)求n的值；

　(2)现从甲、乙两盒各随机抽取1个小球，抽得红球的得分为其标号数；抽得黑球，若标号数为奇数，则得分为1，若标号数为偶数，则得分为零，设被抽取的2个小球得分之和为ξ，求ξ的数学期望Eξ．

16、(本小题满分12分)

已知函数f(x)=[2sin(x+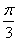)+sinx]cosx－sin2x．

(1)若函数y=f(x)的图像关于直线x=a(a>0)对称，求a的最小值；

(2)若存在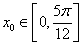，使mf(x0)－2=0成立，求实数m的取值范围．

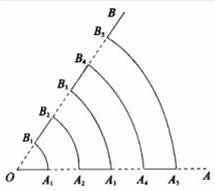
15、如图所示，已知∠AOB=1rad，点A1，A2，…在OA上，B1，B2，…在OB上，其中的每一个实线段和虚线段均为1个单位，一个动点M从O点出发，沿着实线段和以O为圆心的圆弧匀速运动，速度为1单位/秒，则质点M到达A10点处所需要的时间为____秒．

14、已知曲线方程f(x)=sin2x+2ax(a∈R)，若对任意实数m，直线l：x+y+m=0都不是曲线y=f(x)的切线，则a的取值范围为__________．

13、已知函数f(x)是区间[－1，+∞)上的连续函数，当x≠0时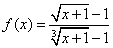，，则f(0)等于__________．

12、设x，y，z是正实数，满足xy+z=(x+z)(y+z)，则xyz的最大值是__________．

11、已知f(x)=|x+3|+|x－7|的最小值为m，则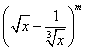展开式中的常数项是__________．

10、定义区间(c，d)，[c，d)，(c，d]，[c，d]的长度均为d－c，其中d>c，已知实数a>b，则满足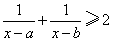的x构成的区间长度之和为(　)

A．1　　　　　　　B．a－b

C．a+b　　　　　　 D．2

第Ⅱ卷(非选择题，共100分)

9、取棱长为a的正方体的一个顶点，过从此顶点出发的三条棱的中点作截面，依次进行下去，对正方体的所有顶点都如此操作，所得的各截面与正方体各面共同围成一个多面体，则此多面体：①有12个顶点；②有24条棱；③有12个面；④表面积为3a2；⑤体积为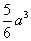．以上结论正确的是(　)

A．①②⑤　　　　　　 B．①②③

C．②④⑤　　　　　　 D．②③④⑤

8、椭圆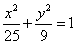上一点P到两焦点的距离之积为m，当m取最大值时，P点坐标为(　)

A．(5，0)，(－5，0)

B．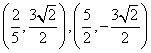

C．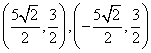

D．(0，－3)，(0，3)