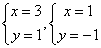6、结合图像，最大值在ax+by+c=0与x+y=4的交点处取得，最小值在ax+by+c=0与x=1的交点处取得，联立方程组，解得，故直线ax+by+c=0过点(3，1)，(1，－1)，所以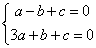，可得，

　故.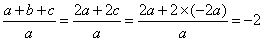

5、f(x+5)≤f(x+4)+1≤f(x+3)+2≤…≤f(x)+5，又f(x+5)≥f(x)+5，

　故f(x+5)=f(x)+5，则f(6)=f(1)+5=6.

4、

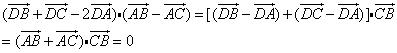
　设D为BC中点，故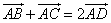，即有AD⊥BC，故AB=AC，△ABC为等腰三角形.

3、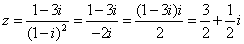，故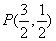在第一象限.

2、由|x－m|<1，可得m－1<x<m+1，所以，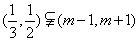

　故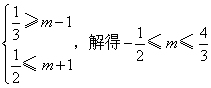，经检验两端点处均符合要求，

　故.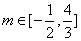

1、利用排除法，易知选C.

21、(本小题满分14分)

　已知数列{an}中的相邻两项a2k－1，a2k是关于x的方程x2－(3k+2k)x+3k·2k=0的两个根，且a2k－1≤a2k(k=1，2，3，…)．

　(1)求a1，a3，a5，a7；

　(2)求数列{an}的前2n项的和S2n；

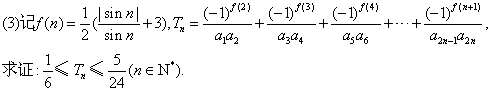
提示：

20、(本小题满分13分)

　设椭圆方程为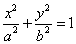(a>b>0)，PQ是过椭圆左焦点F且与x轴不垂直的弦，PQ的中点M到左准线l的距离为d．

　(1)证明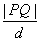：为定值；

　(2)若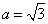，b=1，在左准线上求点R，使△PQR为等边三角形．

19、(本小题满分12分)

　若存在实常数k和b，使得函数f(x)和g(x)对其定义域上的任意实数x分别满足：f(x)≥kx+b和g(x)≤kx+b，则称直线l：y=kx+b为f(x)和g(x)的“隔离直线”．已知h(x)=x2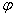，(x)=2elnx(其中e为自然对数的底数)．

　(1)求F(x)=h(x)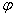－(x)的极值；

　(2)函数h(x)和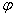(x)是否存在隔离直线?若存在，求出此隔离直线方程；若不存在，请说明理由．

18、(本小题满分12分)

　如图所示，在四棱锥P-ABCD中，PA⊥底面ABCD，∠ABC=∠ADC=90°，∠BAD＝120°，AD=AB=a，若PA=λa(λ>0)．

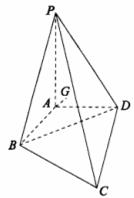
(1)求证：平面PBD⊥平面PAC；

(2)当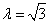时，求点A到平面PDC的距离；

(3)当λ为何值时，点A在平面PBD的射影G恰好是△PBD的重心?