
10.设曲线C: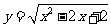 和直线
和直线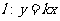 .
.
⑴记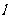 与C的两个交点为A、B,求线段AB中点的轨迹方程;
与C的两个交点为A、B,求线段AB中点的轨迹方程;
⑵若线段AB上的点Q满足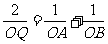 ,求点Q的轨迹方程;
,求点Q的轨迹方程;
⑶在点Q的轨迹上是否存在点Q0,使得经过曲线C的焦点的弦被点Q0平分?证明你的结论.
第18讲 求轨迹方程
[课前热身]
9.求经过定点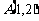 , 以
, 以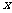 轴为准线,离心率为
轴为准线,离心率为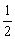 的椭圆下方的顶点的轨迹方程。
的椭圆下方的顶点的轨迹方程。
8.对于顶点在原点的抛物线,给出下列条件①焦点在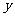 轴上;②焦点在
轴上;②焦点在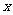 轴上;③抛物线上横坐标为1的点到焦点的距离为6;④抛物线的通径长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。能使这抛物线的方程是
轴上;③抛物线上横坐标为1的点到焦点的距离为6;④抛物线的通径长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。能使这抛物线的方程是 的条件是 (要求填写合适条件的序号)
的条件是 (要求填写合适条件的序号)
7.下列四个命题:
⑴圆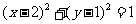 关于点A(1,2)对称的曲线方程是
关于点A(1,2)对称的曲线方程是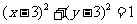 ;
;
⑵以点(2,-3)和点(2,1)为焦点的椭圆方程可以是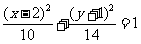 ;
;
⑶顶点在原点,对称轴为坐标轴且过点(―4,―3)的抛物线方程只能是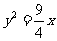 ;
;
⑷双曲线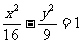 右支上一点P到左准线的距离为18,则P点到右焦点的距离为
右支上一点P到左准线的距离为18,则P点到右焦点的距离为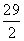 ;
;
以上正确的命题是_______.(将正确命题的序号都填上)
6.椭圆C与椭圆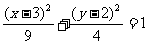 关于直线
关于直线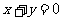 对称,椭圆C的方程是( )
对称,椭圆C的方程是( )
A. 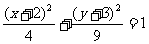 B.
B. 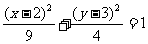
C. 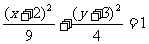 D.
D. 
5.抛物线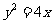 关于直线
关于直线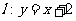 对称的曲线方程是__________.
对称的曲线方程是__________.
4.一动圆M与两定圆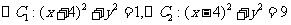 均外切,则动圆圆心M的轨迹方程是_______________.
均外切,则动圆圆心M的轨迹方程是_______________.
3.方程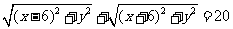 化简的结果是( )
化简的结果是( )
A.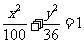 B.
B. 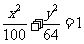 C.
C.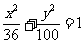 D.
D. 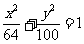
2.点M为抛物线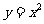 上的一个动点,连结原点O与动点M,以OM为边作一个正方形MNPO,则动点P的轨迹方程为( )
上的一个动点,连结原点O与动点M,以OM为边作一个正方形MNPO,则动点P的轨迹方程为( )
A.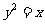 B.
B. 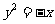 C.
C. 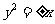 D.
D. 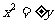
例1用直接法:若曲线上的动点满足的条件是一些几何量的等量关系,则只需直接把这种关系“翻译”成关于动点的坐标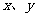 的方程。经化简所得同解的最简方程,即为所求轨迹方程。其一般步骤为:建系--设点--列式--代换--化简--检验。
的方程。经化简所得同解的最简方程,即为所求轨迹方程。其一般步骤为:建系--设点--列式--代换--化简--检验。
例2用圆锥曲线的定义求方程。如果题目中的几何条件能够满足圆、椭圆、双曲线,抛物线的第一、二定义,则直接利用曲线定义写出其轨迹方程。
例3求曲线的轨迹方程是解析几何的两个基本问题之一。求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,通过“坐标互化”将其转化为变量间的关系。在确定了轨迹方程之后,有时需要对方程中的参数进行讨论,因为参数取值的变化会使方程表示不同的曲线,会使其与其他曲线的位置关系不同,会引起另外某些变量取值范围的变化。
例4本题是运用参数法求的轨迹。当动点P的坐标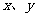 之间的直接关系不易建立时,可适当地选取中间变量
之间的直接关系不易建立时,可适当地选取中间变量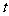 ,并用
,并用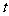 表示动点P的坐标
表示动点P的坐标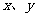 ,从而得到动点轨迹的参数方程
,从而得到动点轨迹的参数方程 ,消去参数
,消去参数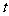 ,便可得到动点P的轨迹普通方程。其中应注意方程的等价性,即由
,便可得到动点P的轨迹普通方程。其中应注意方程的等价性,即由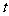 的范围确定出
的范围确定出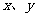 范围。
范围。
冲刺强化训练(18)
班级 姓名_____学号__ 日期 月 日
1.若点M(x,y)满足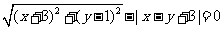 ,则点M的轨迹是( )
,则点M的轨迹是( )
A.圆 B.椭圆 C.双曲线 D抛物线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com