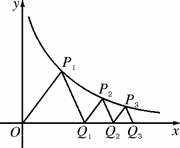
22．(本小题满分12分)已知点P₁、P₂、P₃、…、P_n、…顺次为曲线xy=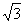(x>0)上的点(如图所示)，点Q₁、Q₂、Q₃、…、Q_n、…顺次为x轴上的点，且△OP₁Q₁、△OP₂Q₂、△Q_n-1P_nQ_n、…均为等边三角形. 记点Q_n(c_n，0)，P_n(a_n，b_n) (其中n∈N^*).

　 (1)求数列{c_n}(n∈N^*)的通项公式；

　 (2)(理)求数列{a_n}(n∈N^* )的通项公式及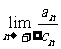的值；

　　　 (文)求数列{a_n}(n∈N^* )的通项公式.

　 (3)(理)求证：(其中n∈N^* ).

(文)求证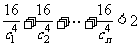：(其中n∈N^* ).

21．(本小题满分12分)已知数列{a_n}满足：a₁=2，a₂=3，2a_n+1=3a_n-a_n-1(n≥2).

(1)求数列{a_n}的通项公式a_n；

(2)求使不等式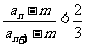成立的所有正整数m、n的值.

20．(本小题满分12分)

　 已知函数f (x)=x+1，点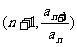(n∈N^*)在y = f ^-1(x)上，且a₁=a₂=1.

　 (1)求数列{a_n}的通项公式；

　 (2)设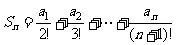，若S_n>m恒成立，求常数m的取值范围.

19．(本小题满分12分)医学上为了确定某种传染病在传播过程病毒细胞的生长规律及其预防方法，通常将这种病毒细胞m个注入一只小白鼠的体内进行试验.

在试验过程中，将病毒细胞的数量(个)与时间(h)的关系记录如下表：

　 已知该种病毒细胞在小白鼠体内的数量超过m×10⁶个时，小白鼠将死亡，但有一种药物对杀死此种病毒有一定的效果，在最初使用此药物的几天内，每次用药可杀死其体内该病毒细胞的98%.

　 (1)为了使小白鼠在试验过程中不死亡，第一次最迟应在何时注射该种药物？

　 (2)第二次最迟应在何时注射该种药物，才能维持小白鼠的生命？(答案精确到小时，参考数据：lg 2=0.301 0)

18．(本小题满分12分)(理)已知数列{a_n}是首项为q、公比为q的等比数列(其中q>0且q≠1)，设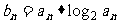(其中n∈N^*).

(1)当q=2时，求数列{b_n}的前n项和为S_n；

　 (2)在(1)的条件下，求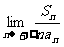的值；

　 (3)当时，在数列{b_n}中，是否存在最小的自然数n，使得对任意的m>n(m∈N^*)，都有b_m>b_n？证明你的结论.

(文)数列{a_n}的通项公式是a_n =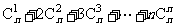(其中n∈N^*)，前n项和为S_n.

(1)化简数列{a_n}的通项公式a_n；

(2)求证：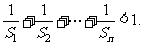

17．(本小题满分10分)

已知数列{a_n}是递增等差数列，前n项和为S_n，a₁=2，且a₁，a₂，a₄成等比数列.

(1)求{a_n}的通项公式；

(2)令，

①当n为何正整数时，T_n>T_n+1？

②若对一切正整数n，总有T_n≤m，求m的取值范围.

16．(理)设正数数列{a_n}的前n项之和是b_n，数列{b_n}前n项之积是c_n，且b_n+c_n=1，则数列中最接近108的项是第　　　 项.

(文)在等比数列{a_n}中，a₁=，公比q=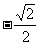，其前n项之和是S_n，x=S₁₀(S₂₀+S₃₀)，y=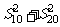，则x，y的大小关系是　　　 .

15．在△ABC中，内角A、B、C的对边分别是a、b、c，且a²，b²，c²成等差数列，则sinB的最大值是　　　　　　　　　 .

14．(理)一张厚度为0.1 mm的矩形纸片，每次将此纸片沿一组对边的中点连线对折，则经过　　　　　　 次这样的折叠后其厚度开始大于100 m(假设这样的折叠是可以实现的，参考数据：lg 2=0.3010).

(文)一种机械设备的价格为200000元，假设维护费第一年为1000元，以后每年增加1000元，当此设备的平均费用为最小时为最佳更新年限，那么此设备的最佳更新年限为　　 　.

13．(理)在正项等比数列{a_n}中，a₂a₈=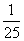，a₁+a₉的最小值是m，且3^a=m，其中a∈(k，k+1)，则整数k=　　　　　 　　.

　 (文)在正项等比数列{a_n}中，a₂a₈=25，a₁+a₉的最小值是m=　　　　　　　 .