
∴M≥ .
.
③当0<b≤3时,2M≥|f′(1)|+|f′(- )|=|3+2b+c|+|c-
)|=|3+2b+c|+|c-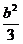 |≥|
|≥|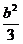 +2b+3|=|
+2b+3|=| (b+3)2|>3,
(b+3)2|>3,
∴M≥ .
.
②当-3≤b≤0时,2M≥|f′(-1)|+|f′(- )|=|3-2b+c|+|c-
)|=|3-2b+c|+|c-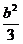 |≥|
|≥|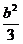 -2b+3|=|
-2b+3|=| (b-3)2|>3,
(b-3)2|>3,
从而M≥ . 11分
. 11分
①若|- |>1,则M应是|f′(-1)|和|f′(1)|中最大的一个,
|>1,则M应是|f′(-1)|和|f′(1)|中最大的一个,
∴2M≥|f′(-1)|+|f′(1)|=|3-2b+c|+|3+2b+c|≥|4b|>12,
∴M>6,
(3)证法一:∵|f′(x)|=|3(x+ )2+c-
)2+c-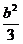 |,
|,
又∵b≠0,△<0.
从而方程3t2+2bt+b2=0无解,
因此不存在t,使f′(t)=c-b2,
即f(x)的图象不存在与直线(b2-c)x+y+1=0平行的切线. 9分
即3t2+2bt+b2=0.
∵△=4(b2-3b2)=-8b2,
从而符合在x=1时,f(x)有极值.∴ 4分
4分
(2)假设f(x)图象在x=t处的切线与直线(b2-c)x+y+1=0平行,
∵f′(t)=3t2+2bt+c,
直线(b2-c)x+y+1=0的斜率为c-b2,
∴3t2+2bt+c=c-b2,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com