
21.在数列 中,已知
中,已知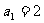 ,
,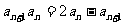 .
.
(1)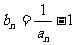 ,求证数列
,求证数列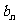 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前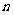 项和
项和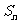 。
。
20.(本大题12分)
已知函数
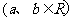 。
。
(I)若函数 在x=1处有极值-4,求
在x=1处有极值-4,求 的单调区间;
的单调区间;
(II)在(I)的条件下,求函数 在[-1,2]上的最值。
在[-1,2]上的最值。
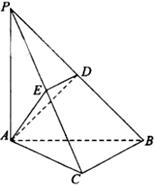
19.如图,在三棱锥 中,
中, ,
,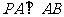 ,
,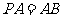 ,
,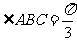 ,
,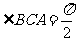 , 点
, 点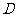 ,
,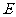 分别在棱
分别在棱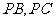 上,且
上,且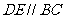 ,
,
(Ⅰ)求证: 平面
平面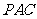 ;
;
 (Ⅱ)当
(Ⅱ)当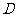 为
为 的中点时,求
的中点时,求 与平面
与平面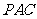 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点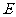 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
17.(本大题10分)
 一气球以V(m/s)的速度由地面上升,10分钟后由观察点P测得气球在P的正东方向S处,仰角为
一气球以V(m/s)的速度由地面上升,10分钟后由观察点P测得气球在P的正东方向S处,仰角为 ;再过10分钟后,测得气球在P的东偏北
;再过10分钟后,测得气球在P的东偏北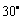 方向T处,其仰角为
方向T处,其仰角为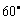 (如图,其中Q、R分别为气球在S、T处时的正投影).求风向和风速(风速用V表示).
(如图,其中Q、R分别为气球在S、T处时的正投影).求风向和风速(风速用V表示).
18(本大题12分)
为了迎接2009年10月1日建国60周年,某城市为举办的大型庆典活动准备了四种保证安全的方案,列表如下:
|
方案 |
A |
B |
C |
D |
|
经费 |
300万元 |
400万元 |
500万元 |
600万元 |
|
安全系数 |
0.6 |
0.7 |
0.8 |
0.9 |
其中安全系数表示实施此方案能保证安全的系数,每种方案相互独立,每种方案既可独立用,又可以与其它方案合用,合用时,至少有一种方案就能保证整个活动的安全
(I)求A、B两种方案合用,能保证安全的概率;
(II)若总经费在1200万元内(含1200万元),如何组合实施方案可以使安全系数最高?
16.关于函数
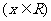 的如下结论:①
的如下结论:① 是偶函数;②函数
是偶函数;②函数 的值域为
的值域为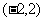 ;③若
;③若 ≠
≠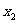 ,则一定有
,则一定有 ≠
≠ ④函数
④函数 的图象关于直线
的图象关于直线 对称;其中正确结论的序号有_________。(请将你认为正确的结论的序号都填上)
对称;其中正确结论的序号有_________。(请将你认为正确的结论的序号都填上)
15.已知椭圆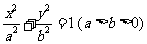 的左
的左 焦点为
焦点为 ,右顶点为
,右顶点为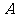 ,点
,点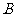 在椭圆上,且
在椭圆上,且 轴, 直线
轴, 直线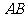 交
交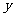 轴于点
轴于点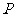 .若
.若 ,则椭圆的离心率是__________
,则椭圆的离心率是__________
14.在 中,已知
中,已知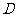 是
是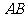 边上一点,若
边上一点,若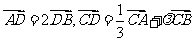 ,则
,则 等于
等于
_________________
13.设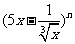 的展开式的各项系数之和为M,二项式系数之和为N,若M-N=240,则展开式中的常数项为_________
的展开式的各项系数之和为M,二项式系数之和为N,若M-N=240,则展开式中的常数项为_________
12.有以下四个命题①设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,],则点P到曲线y=f(x)对称轴距离的取值范围为 [0,];②一质点沿直线运动,如果由始点起经过t称后的位移为 ,那么速度为零的时刻只有1秒末;③若函数
,那么速度为零的时刻只有1秒末;③若函数 在区间
在区间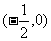 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是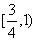 ;④定义在
;④定义在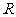 上的偶函数
上的偶函数 ,满足
,满足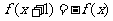 ,则
,则 的图象关于
的图象关于 对称;其中正确的有 ( )
对称;其中正确的有 ( )
A.0 B. 1 C. 2 D. 3
第Ⅱ卷
|
11.设连结双曲线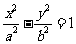 与
与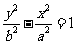 (
(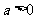 ,
,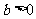 )的
)的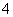 个顶点的四边形面积为
个顶点的四边形面积为 ,连结其
,连结其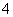 个焦点
个焦点 的四边形面积为
的四边形面积为 ,则
,则 的最大值为 ( )
的最大值为 ( )
A.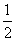 B.
B. C.
C.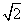 D.
D.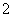
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com