
5、在正方形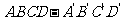 中,过对角线
中,过对角线 的一个平面交
的一个平面交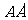 于
于 ,交
,交 于
于 ,则①四边形
,则①四边形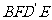 一定是平行四边形;②四边形
一定是平行四边形;②四边形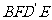 有可能是正方形;③四边形
有可能是正方形;③四边形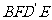 在底面
在底面 内的投影一定是正方形;④四边形
内的投影一定是正方形;④四边形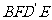 有可能垂直于平面
有可能垂直于平面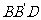 。以上结论正确的为 。(写出所有正确结论的编号)
。以上结论正确的为 。(写出所有正确结论的编号)
[例题探究]
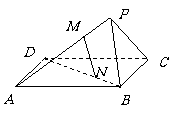 例1、已知
例1、已知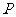 是正方形
是正方形 平面外一点,
平面外一点,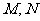 分别为
分别为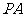 和
和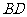 上的点,且
上的点,且 。求证:直线
。求证:直线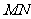 ∥
∥ 。
。
 例2、如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,
例2、如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,
AB=5,AA1=4,点D是AB的中点,
(1)求证:AC⊥BC1;
(2)求证:AC 1//平面CDB1;
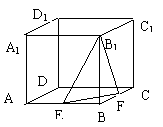
例3、长方体ABCD-A1B1C1D1中,E、F分别是线段B1D1、A1B上的点,且D1E=2EB1,BF=2FA1。
(1)求证:EF∥AC1
(2)若EF是两异面直线B1D1、A1B的公垂线段,求证该长方体为正方体。
 备用题、在正方体
备用题、在正方体 中,
中, 分别是
分别是 的中点,试问在棱
的中点,试问在棱 上能否找到一点
上能否找到一点 ,使
,使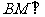
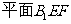 ?若能,确定点
?若能,确定点 的位置;若不能,说明理由。
的位置;若不能,说明理由。
[方法点拨]
4、已知 是不同的直线,
是不同的直线, 是不重合的平面,给出命题:①
是不重合的平面,给出命题:① 则
则 ;②若
;②若 则
则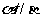 ;③若
;③若 ,则
,则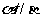 ;④
;④ 是两条异面直线,若
是两条异面直线,若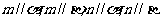 ,则
,则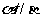 。上面的命题中,真命题的序号是 (写出所有真命题的序号)
。上面的命题中,真命题的序号是 (写出所有真命题的序号)
3、在正四面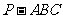 中,
中,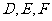 分别是
分别是 的中点,则下面结论中不成立的是( )
的中点,则下面结论中不成立的是( )
A、 平面
平面 B、
B、 平面
平面
C、平面 ⊥平面
⊥平面 D、平面
D、平面 ⊥平面
⊥平面
2、已知 是两个平面,
是两个平面, 是两条直线,则下列命题不正确的是:( )
是两条直线,则下列命题不正确的是:( )
A.若 ∥
∥ ,
,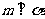 ,则
,则 B.若
B.若 ∥
∥ ,
,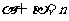 ,则
,则 ∥
∥
C.若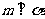 ,
, ,则
,则 ∥
∥ D.若
D.若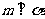 ,
,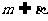 ,则
,则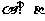
1、在正方体 中,
中, 是异面直线
是异面直线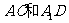 的公垂线,则
的公垂线,则 和
和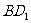 的关系是( )
的关系是( )
A.相交垂直 B.相交但不垂直 C.异面垂直 D.互相平行
4、培养学生用向量的代数推理能力解决立几中探索性问题的意识。
[课前热身]
3、培养学生空间想象能力、逻辑推理能力;
2、学会运用判定及性质定理以及向量方法解决平行与垂直的问题;
1、理解平行与垂直的有关概念及熟练掌握判定定理和性质定理;
22.设向量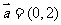
 ,过定点A(0,-2),以
,过定点A(0,-2),以 方向向量的直线与经过点B(0,2),以向量
方向向量的直线与经过点B(0,2),以向量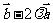 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中 ,
,
(I)求点P的轨迹C的方程;
(II)设过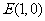 的直线
的直线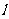 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com