
3.(文) 的定义域是( )
的定义域是( )
A.  B.
B.
C. D.
D.
(理)不等式 的解集是( )
的解集是( )
A. B.
B. C.
C. D.
D.
2.(文)等比数列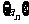 中,
中, ,则
,则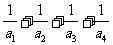 =
=
A. B.
B. C.
C.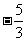 D.
D.
(理)数列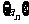 中有
中有 ,
, ,且等式对
,且等式对 对于任意
对于任意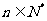 成立,则
成立,则 ( )
( )
A.5032 B.5044 C.5048 D.5050
1.若数列{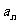 }满足
}满足 ,
, 且
且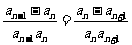 (
( )则
)则 等于( )
等于( )
A、 B、
B、 C、
C、 D、
D、
8、(Ⅰ)证明 因为底面ABCD是菱形,∠ABC=60°,
 所以AB=AD=AC=a, 在△PAB中,
所以AB=AD=AC=a, 在△PAB中,
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
(Ⅱ)解 作EG//PA交AD于G,
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连结EH,
则EH⊥AC,∠EHG即为二面角 的平面角.
的平面角.
又PE : ED=2 : 1,所以
从而 

(Ⅲ)解法一 以A为坐标原点,直线AD、AP分别为y轴、z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系如图.由题设条件,相关各点的坐标分别为



所以 


设点F是棱PC上的点, 则
则

 令
令  得
得

解得  即
即  时,
时,
亦即,F是PC的中点时, 、
、 、
、 共面.
共面.
又 BF 平面AEC,所以当F是棱PC的中点时,BF//平面AEC.
平面AEC,所以当F是棱PC的中点时,BF//平面AEC.
解法二 当F是棱PC的中点时,BF//平面AEC,证明如下,
证法一 取PE的中点M,连结FM,则FM//CE. ①
 由
由  知E是MD的中点.
知E是MD的中点.
连结BM、BD,设BD AC=O,则O为BD的中点.
AC=O,则O为BD的中点.
所以 BM//OE. ②
由①、②知,平面BFM//平面AEC.
又 BF 平面BFM,所以BF//平面AEC.
平面BFM,所以BF//平面AEC.
证法二
因为 

所以  、
、 、
、 共面.又 BF
共面.又 BF 平面ABC,从而BF//平面AEC.
平面ABC,从而BF//平面AEC.
7、解:(1)取B’D’的中点E,连CE,可以证明OA’∥CE,从而可证得OA’∥平面B’CD’

 (2)取A’B’的中点M,则CM⊥平面 AB’,AM为C’A在面 AB’内的射影。如图,
(2)取A’B’的中点M,则CM⊥平面 AB’,AM为C’A在面 AB’内的射影。如图,
只要∠ABF=∠A’AM,
就有C’A⊥平面BDF。由相似三角形知识可得:
 此时
此时 。
。
6.解法一
(1)
证明:延长PG交 AB于D,过D作DM 于M。
于M。
由G是三角形APB的重心  D是AB中点。
D是AB中点。
又AP PB
PB  DM // AP
DM // AP
 M是PB的中点
M是PB的中点


 GF // DM
GF // DM
 GF
GF PB
PB
又CP PA, CP
PA, CP PB
PB  CP
CP 面APB
面APB  CP
CP GF
GF
又PB交CP于P  GF
GF 面PBC
面PBC
又GF 面GEF
面GEF  面GEF
面GEF 面PBC
面PBC
(2) 解: P-ABC是正三棱锥
P-ABC是正三棱锥  PC=PB= a
PC=PB= a
 BC=
BC= a
a
 BE=
BE= , BF=
, BF= ,
, 


 ∽
∽ ,
,  EF
EF BC,
BC,
又GF 面PBC
面PBC  GE
GE BC
BC
过G点作GH // AB 交PB于H, 连EH: 

 EH // Pc
EH // Pc  EH
EH 面APB, 又PG
面APB, 又PG AB
AB  GH
GH
 EG
EG PG
PG
 EG是PG和BC的公垂线。
EG是PG和BC的公垂线。
解法二
证明:(1)将正三棱锥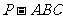 如图放置在坐标系中,使
如图放置在坐标系中,使 点为坐标原点,
点为坐标原点,
并设 ,
,
则



 ,
,
 .由于
.由于 平面
平面 ,
,

 平面
平面 ,于是平面
,于是平面
 平面
平面 。
。
(2)


 是
是 和
和 的公垂线。
的公垂线。
1、D 2、D 3、A 4、(1)③⑤(2)②⑤ 5、
1、D 2、B 3、C 4、③④ 5、①③④
例1:证法一 证明:在面AC中,过N作BC的平行线交AB于Q,
则NQ // BC,连结MQ. 在面AC中,
在面APB中,
 MQ // PB
MQ // PB
又 NQ // BC,
NQ // BC, 
 面MNQ // 面PBC
面MNQ // 面PBC
 直线MN
直线MN 面MNQ
面MNQ
 MN // 面PBC
MN // 面PBC
证法二
证明:


在BC上取一点E,使 ,
,
 MN//PE,
MN//PE, MN//平面PBC。
MN//平面PBC。
 例2(1)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
例2(1)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(2)解法1 设CB1与C1B的交点为E,连结DE,
∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,∵ DE 平面CDB1,AC1
平面CDB1,AC1 平面CDB1,∴ AC1//平面CDB1;
平面CDB1,∴ AC1//平面CDB1;
解法2 取A1B1中点M,连结C1M,AM、
DM,易证四边形ADB1M,CDMC1是平
行四边形,得到AM//DB1,C1M//CD,从而得到AM//平面CDB1,C1M//平面CDB1
(3)∠DEC为所求的异面直线所成的角。其余弦值为 .
.
 例3:解法一:(1)取A1B1中点M,连结AM、MC1,设MC1与B1D1相交于点E'。∵
例3:解法一:(1)取A1B1中点M,连结AM、MC1,设MC1与B1D1相交于点E'。∵ ,∴B1E=2 E′D1,又∵D1E=2EB1,∴E′与E重合,∴M、E、C1共线,且
,∴B1E=2 E′D1,又∵D1E=2EB1,∴E′与E重合,∴M、E、C1共线,且 。同理,M、F、A三点共线,
。同理,M、F、A三点共线,
且 。∴
。∴ ,∴EF∥AC1,
,∴EF∥AC1,
(2)连结A1C1,
∵EF是两异面直线B1D1、A1B1的公垂线段,∴EF⊥B1D1,EF⊥A1B。前面已证EF∥AC1,∴AC1⊥B1D1。
又∵AA1⊥平面A1B1C1D1,∴A1C1⊥B1D1,∴A1B1C1D1为正方形,同理,A1B1BA为正方形。∴A1B1=A1A。 ∴该长方体为正方体。
解法二:(1)如图,以D为原点,DA、DC、DD1所在直线为x轴、y轴、z轴,建立空间直角坐标系。设DA=a,DC=b,DD1=c,则E( ),F(
),F( ),
), ,
, 。
。 ,
, ,∴
,∴ ,∴
,∴ ∥
∥ 。
。
∵FE与AC1不共线,∴FE∥AC1。
(2)∵D1(0,0,c),B1(a,b,c),A1(a,0,c),B(a,b,0),
 ∴
∴ =(a,b,0),
=(a,b,0), =(0,b,-c),
=(0,b,-c),
∵EF是两异面直线B1D1、A1B的公垂线段,
∴EF⊥B1D1,EF⊥A1B。
∴ ,
, ,
,
∴ ,b2-c2=0,∴a=b=c。
,b2-c2=0,∴a=b=c。
∴该长方体为正方体。
解法三:(1)设 ,
, ,
,
则

又∵ , ∴
, ∴ ∴A1C∥FE
∴A1C∥FE
(2)由题意知EF是B1D、A1B的公垂线。
即:AC1⊥B1D且AC1⊥A1B


 =0
=0
 =0
=0
即

 =0
=0
∴ ∴该长方体为正方体。
∴该长方体为正方体。
备用题:解法一 作法:①B作BG
 交
交 于G;②过G作GM // AD交
于G;②过G作GM // AD交 于M;
于M;
③连BM,则BM即为所求作 证明: 连BD 正方体ABCD- 中,E,F为AB和BC的中点
中,E,F为AB和BC的中点 
 ,又
,又 面ABCD
面ABCD  EF
EF BM
BM
又 GM // AD
GM // AD  面
面 而
而

又
 面
面
解法二
解:以D为原点,DA为x轴,DC为y轴, 为z轴建立空间直角坐标系,
为z轴建立空间直角坐标系,
设正方体棱长为1,则 , 设M
, 设M ,于是
,于是 ,
, ,
, ,
,

 恒成立,要使BM
恒成立,要使BM 平面
平面 ,只需
,只需 ,
,
即 ,而
,而
故当M是 的中点时,BM
的中点时,BM 。
。
冲刺强化训练(21)
8、 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD= ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(1)证明PA⊥平面ABCD;
(2)求二面角 的大小;
的大小;
(3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
第21讲 平行与垂直问题
[课前热身]
7、如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且∠ABC=600,侧棱AA1的长等于3a,O为底面ABCD的对角线的交点。
(1)求证:OA1//平面B1CD1;
 (2)在棱AA1上取一点F,问AF为何值时,C1A⊥平面BDF?
(2)在棱AA1上取一点F,问AF为何值时,C1A⊥平面BDF?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com