4、生活中的优化问题

会用导数解决实际问题。

3、导数在研究函数中的应用

(1)了解函数的单调性与导数的关系；能利用导数研究函数的单调性，会求函数的单调区间(对多项式函数不超过三次)。

(2)了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值(对多项式函数不超过三次)；会求闭区间上函数的最大值、最小值(对多项式函数不超过三次)。

2、导数的运算

(1)能根据导数的定义求函数y=C(C为常数)，y=x,y=x²,y=x^-1　，的导数。

(2)能利用以下给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数，能求简单复合函数(仅限于形如的复合函数)的导数。

常见的基本初等函数的导数公式:

(C为常数)　　 　 ()

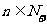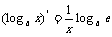
常用的导数运算法则：

法则1：

法则2：

法则3：　

1、导数的概念及其几何意义

(1)了解导数概念的实际背景．

(2)理解导数的几何意义．

2、空间向量的应用

　(1)理解直线的方向向量及平面的法向量。

　(2)能用向量语言表述线线、线面、面面的平行和垂直关系。

　(3)能用向量方法证明立体几何中有关线面位置关系的一些简单定理(包括三垂线定理)。

　(4)能用向量方法解决简单的直线与直线、直线与平面、平面与平面的夹角计算问题，了解空间向量方法在研究简单立体几何问题中的作用。

1、空间向量及其运算

　(1)了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示。

　(2)掌握空间向量的线性运算及其坐标表示。

(3)掌握空间向量的数量积及其坐标表示，能用向量的数量积判断向量的共线和垂直。

2、曲线与方程

了解方程的曲线与曲线的方程的对应关系。

1、圆锥曲线

(1)了解圆锥曲线的实际背景，了解圆锥曲线在刻画现实世界和解决实际问题中的作用。

(2)掌握椭圆、抛物线的定义、几何图形、标准方程和简单的几何性质。

(3)了解双曲线的定义、几何图形和标准方程，知道其简单的几何性质。

(4)了解圆锥曲线的简单应用。

(5)理解数形结合的思想。

3、全称量词与存在量词

(1)理解全称量词和存在量词的意义。

(2)能正确地对含一个量词的命题进行否定。

2、简单逻辑联结词

了解逻辑联结词“或”、“且”、“非”的含义。