22．(本题满分14分)

　　 已知实数a≥，函数y=e^x-ax区间[-ln3，o)上的增函数，设函数f(x)=ax³-x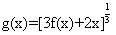　 　

　　 (I)求a的值并写出g(x)的表达式；

　　 (Ⅱ)求证：当x>o时，；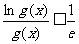

　　 (Ⅲ).

21．(本题满分1 2分)

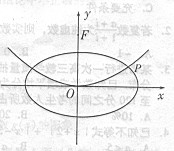
　　 如图，抛物线C1：x²=2py(p>0)的焦点为F，椭圆

　 C2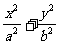：=l(a>b>o)的离心率e=，c1与c2在

　 第一象限的交点为p(，)．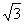

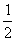　　 (I)求抛物线C1及椭圆C2的方程；

　　 (Ⅱ)已知直线l：y=kx+t(k≠0，t≠0)与椭圆C2交于不同两点A、B，

点m满足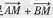=0，直线FM的斜率为k1，且k·k1=2，求t的取值范围。

　 1 7．(本题满分1 2分)

　　 已知钝角△ABC中，角A、B、C的对边分别为a、b、c，且(在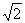a一c)cosB=bcosC．

　 　(I)求角B的大小；

　　 (Ⅱ)设向量m=(cos2A+1，cosA)，n=(1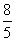，-)，且m⊥n，求tan(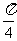+A)的值．

1 8．(本题满分1 2分)

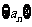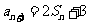　　 已知数列的前n项积且；数列{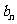}为等差数列，且公差d>0，．

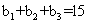　 (I)求数列{an}的通项公式；

　 (Ⅱ)若成等比数列，求数列{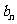 }的前n项和．

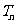1 9．(本题满分1 2分)

　　 如图甲，直角梯形ABCD中，AB ⊥AD，AD∥BC，F为AD中点，E在BC上，且EF∥AB，已知AB=AD=CE=2，现沿EF把四边形CDFE折起如图乙，使平面CDFE⊥平面ABEF

(I)求证：AD∥平面BCE；

(Ⅱ)求证：AB⊥平面BCE；

(Ⅲ求三棱锥C-ADE的体积。

20．(本题满分1 2分)

　 某工厂有工人500名，记35岁以上(含35岁)的为A类工人，不足35岁的为B类工人，为调查该厂工人的个人文化素质状况，现用分层抽样的方法从A、B两类工人中分别抽取了40人、60人进行测试．

　　 (I)求该工厂A、B两类工人各有多少人?

　　 (Ⅱ)经过测试，得到以下三个数据图表：

　　 图一：75分以上A、B两类工人成绩的茎叶图

(茎、叶分别是十位和个位上的数字)(如右图)

　①先填写频率分布表(表一)中的六个空格，然后将频率分布直方图(图二)补充完整；

　②该厂拟定从参加考试的79分以上(含79分)的B类工人中随机抽取2人参加高级技工培训班，求抽到的2人分数都在80分以上的概率

16．设函数f(x)是定义在R上的偶函数，且对任意的x∈R恒有f(x+1)=f(x-1)，已知

　当x∈[0，1]时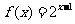，则

　　 ①2是函数f(x)的周期；

　　 ②函数f(x)在(2，3)上是增函数；

　　 ③函数f(x)的最大值是1，最小值是0；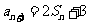

　　 ④直线x=2是函数f(x)图像的对称轴．

　　 其中所有正确命题的序号是　　　　　　　　 　　，

15．正三棱锥P一ABC的四个顶点在同一球面上，已知AB=2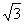，PA=4，则此球的表　　 面积等于　　　　　　　　　

l 3．已知a=(3，-1)，b=(1，-2)若(-a+b)∥(a+kb)，则实数k的值是 　　　　　　　

14．若双曲线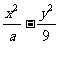 =1的一条渐近线的倾斜角为60⁰，则双曲线的离心率等于　　

10．函数f(x)=lnx-x²+2x+5的零点的个数是

　　 A．0　　 B．1　　 C.2　　 D．3

　l1．已知f(x)=sin(x+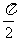)，g(x)=cos(x-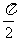)，则下列结论中不正确的是

　　 A．函数y=f(x)·g(x)的最小正周期为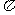

　　 B．函数y=f(x)·g(x)的最大值为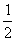

　　 C.函数y=f(x)·g(x)的图象关于点(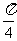，0)成中心对称

　　 D．将函数f(x)的图象向右平移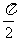个单位后得到函数g(x)的图象

1 2.某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨、B原料2吨；

　　 生产每吨乙产品要用A原料1吨、B原料3吨．销售每吨甲产品可获得利润1万

　　 元，每吨乙产品可获得利润3万元，该企业在某个生产周期内甲产品至少生产1

　　 吨，乙产品至少生产2吨，消耗A原料不超过1 3吨，消耗B原料不超过1 8吨，那

　　 么该企业在这个生产周期内获得最大利润时甲产品的产量应是

　　 A．1吨　　 B．2吨　　 C．3吨　　 D．吨

第Ⅱ卷　 (非选择题共90分)

9.圆心在曲线y=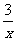 (x>o)上，且与直线3x+4y+3=0相切的面积最小的圆的方程为

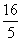A．(x-1)²+(y-3)²=()2 　　B．(x-3)²+(y-1)²=()²

C．(x-2)²+(y-)²=9　　　 D．(x-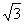)²+(y-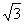)²=9

8.若曲线f(x)=x.·sinx+1在x=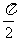处的切线与直线ax+2y+1=0互相垂直，则实数a等于

　　 A．-2　　 B．-1　　 C．1　　 D．2

7.已知f(x)=a^x-2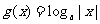， (a>0且a≠1)，若f(4)·g(-4)<0，则y=f(x)，y=g(x)在同一坐标系内的大致图象是