
8.已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点。
(1)求平面PCD与平面ABCD所成二面角的大小;
(2)求证平面MND⊥平面PCD;
(3)求当AB的长度变化时异面直线PC与AD所成角的取值范围。
第22讲 空间角与距离(1)
[课前热身]1 B 2 C 3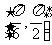 4
4 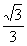
[例题探究]
例1.(1)∵AB⊥平面BC1,PC 平面BC1,∴AB⊥PC
平面BC1,∴AB⊥PC
在矩形BCC1B1 中,BC=2,BB1=1,P为B1C1的中点,∴PC⊥PB
∴PC⊥平面ABP,∴∠CAP为直线AC与平面ABP所成的角
∵PC=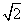 ,AC=
,AC= ,∴在Rt△APC中,∠CAP=300
,∴在Rt△APC中,∠CAP=300
∴直线AC与平面ABP所成的角为300
(2)取A1D1中点Q,连结AQ、CQ,在正四棱柱中,有AQ∥BP,
∴∠CAQ为异面直线AC与BP所成的角
在△ACQ中,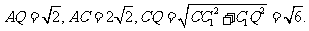
∴∠CAQ=600
∴异面直线AC与BP所成的角为600 (也可用向量法)
(3)过点B作BH⊥AP于H, 由题(1) PC⊥平面ABP,∴PC⊥BH
∴BH⊥平面APC
∴BH的长即为点B到平面APC的距离
在Rt△ABP中,AB=2,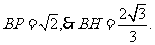
例2:(1)证:因为四边形BCC1B1是矩形,∴BC⊥BB1,又∵AB⊥BC,∴BC⊥平面A1ABB1。
∵BC 平面CA1B,∴平面CA1B⊥平面A1ABB1。
平面CA1B,∴平面CA1B⊥平面A1ABB1。
(2)解:过A1作A1D⊥B1B于D,连接DC,∵BC⊥平面A1ABB1,
∴BC⊥A1D,∴A1D⊥平面BCC1B1,故∠A1CD为直线A1C与平面BCC1B1所成的角。
在矩形BCC1B1中,DC=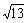 ,因为四边形A1ABB1是菱形,∠A1AB=60°,CB=3,AB=4,∴A1D=
,因为四边形A1ABB1是菱形,∠A1AB=60°,CB=3,AB=4,∴A1D=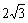 ,∴tan∠A1CD=
,∴tan∠A1CD=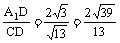 。
。
(3)∵B1C1∥BC1,∴B1C1∥平面A1BC,∴C1到平面A1BC的距离即为B1到平面A1BC的距离。连结AB1,AB1与A1B交于点O,∵四边形A1ABB1是菱形,∴B1O⊥A1B,∵CA1B⊥平面A1ABB1,∴B1O⊥平面A1BC,∴B1O即为C1到平面A1BC的距离。∵B1O=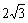 ,∴C1到平面A1BC的距离为
,∴C1到平面A1BC的距离为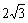 。
。
例3.:在长方体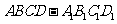 中,以
中,以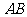 所在的直线为
所在的直线为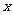 轴,以
轴,以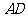 所在的直线为
所在的直线为 轴,
轴,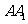 所在的直线为
所在的直线为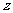 轴建立如图示空间直角坐标系
轴建立如图示空间直角坐标系
由已知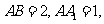 可得
可得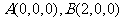 ,
,
又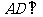 平面
平面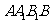 ,从而
,从而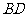 与平面
与平面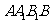 所成的角为
所成的角为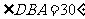 ,又
,又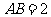 ,
,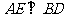 ,
, 从而易得
从而易得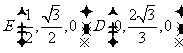
(1)因为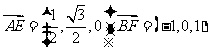 所以
所以 =
=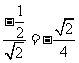
易知异面直线 所成的角为
所成的角为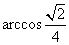
(2)易知平面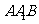 的一个法向量
的一个法向量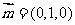 设
设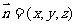 是平面
是平面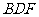 的一个法向量,
的一个法向量,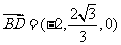 由
由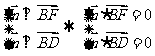
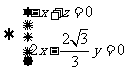
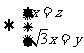
即 所以
所以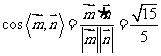 即平面
即平面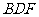 与平面
与平面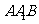 所成的二面角的大小(锐角)为
所成的二面角的大小(锐角)为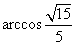
(3)点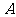 到平面
到平面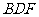 的距离,即
的距离,即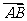 在平面
在平面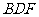 的法向量
的法向量 上的投影的绝对值,
上的投影的绝对值,
所以距离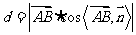 =
=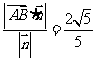 所以点
所以点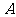 到平面
到平面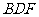 的距离为
的距离为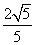
冲刺强化训练(22)
7、如图,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为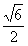 。
。
(1)求侧面PAD 与底面ABCD所成二面角的大小 ;
(2)若E 是PB 中点,求异面直线PD与AE所成的角的正切值 ;
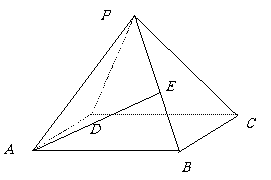 (3)在侧面PAD上寻找一点F使EF⊥侧面PBC,试确定F的位置并证明。
(3)在侧面PAD上寻找一点F使EF⊥侧面PBC,试确定F的位置并证明。
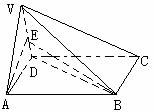
6、在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD。
(1)证明AB⊥平面VAD;
(2)求面VAD与面VDB所成的二面角的大小。
5、锐二面角α-l-β的棱l上一点A,射线AB α,且与棱成45°角,
α,且与棱成45°角,
与β成30°角,则二面角α-l-β的大小是( )
A、30° B、45° C、60° D、90°
4、将正方体的纸盒展开(如图),直线AB、CD在原正方体中的位置关系是( )
A、平行 B 、垂直 C、且成 角 D 、 异面且成
角 D 、 异面且成 角
角
3.在正三棱柱ABC-A1B1C1中,若AB=2,A A1=1,则点A到平面A1BC的距离为( )
 A、
A、 B、
B、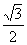 C、
C、 D、
D、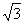
2、在正三棱柱ABC-A1B1C1中,若AB= BB1,则AB1与C1B所成的角的大小为()
BB1,则AB1与C1B所成的角的大小为()
A.60° B.90° C.105° D.75°
1、空间四边形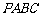 中,若
中,若 ,则
,则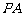 与平面
与平面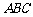 所成角的余弦值
( )
所成角的余弦值
( )
A. B.
B.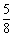 C.
C.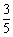 D.
D.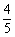
3、二面角的平面角的基本作法有:定义法,三垂线定理法,垂面法。点到面的距离通常在面面垂直背景下向线作垂线得到线面垂直得射影。另空间距离和角的求解应遵循:一作二证三计算。
冲刺强化训练(22)
班级 姓名 学号 成绩 日期 月 日
2、求线面角关键是找、作线与面垂直,通常是先寻找面面垂直,得到线面垂直;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com