
22.(12分)曲线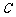 是中心在原点,焦点在
是中心在原点,焦点在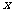 轴上的双
轴上的双 曲线,已知它的一个焦点
曲线,已知它的一个焦点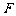 的
的
坐标为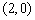 ,一条渐近线的方程为
,一条渐近线的方程为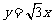 ,过焦点
,过焦点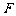 作直线交曲线
作直线交曲线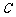 的右支于
的右支于
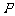 、
、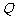 两点,
两点,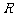 是弦
是弦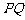 的中点.
的中点.
⑴ 求曲线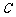 的方程;
的方程;
⑵ 若在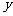 轴左侧能作出直线
轴左侧能作出直线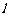 :
: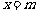 ,使以线段
,使以线段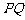 为直径的圆与直线
为直径的圆与直线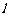 相切,
相切,
求实数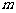 的取值范围.
的取值范围.

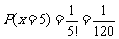 ;
;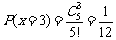 ;
;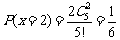 ;
;
 ;
;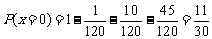 ,
,
∴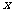 的分布列为:
的分布列为:
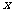
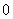
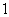
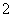
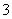
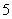
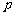
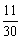
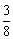
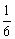
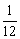
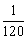
………………………………10分
 ⑵ ∵侧面
⑵ ∵侧面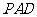
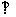 底面
底面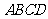 ,又
,又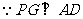 ,
,
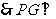 底面
底面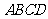 .
.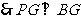 .
.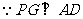 .
.
∴直线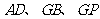 两两互相垂直,
……………………8分
两两互相垂直,
……………………8分
 ⑵ 由⑴知,
⑵ 由⑴知,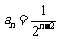 ,则
,则
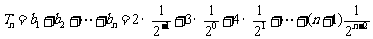 ①
①
∴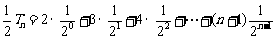 ②
②
①-②,得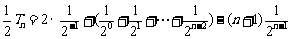
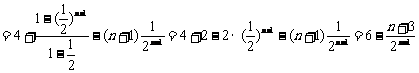 ,……9分
,……9分
∴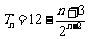 .
……………………………
.
…………………………… ………………………12分
………………………12分
 当
当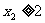 时,
时,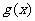 在[0,2]上单调递减,最大值为
在[0,2]上单调递减,最大值为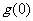 ,
,
所以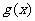 在[0,2]上的最大值只能为
在[0,2]上的最大值只能为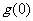 或
或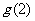 ;
;
又已知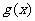 在x=0处取得最大值,所以
在x=0处取得最大值,所以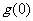

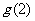
即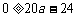 解得
解得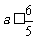 ,∴
,∴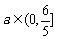 . ……………………
. …………………… ………………12分
………………12分
 ∴当
∴当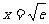 时有
时有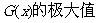 为0,也就是最大值为0.
为0,也就是最大值为0.
从而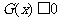 ,即
,即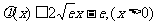
 恒成立.
恒成立.
故函数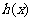 和
和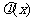 存在唯一的“隔离直线”
存在唯一的“隔离直线”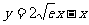 .……………12分
.……………12分
[文科]文科22题为理科21题.
⒘(10分)已知向量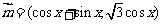 ,
,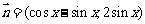 ,设函数
,设函数
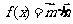 ,若角
,若角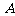 是锐角三角形的最大内角,求
是锐角三角形的最大内角,求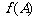 的取值范围.
的取值范围.
⒙(12分)将编号为1,2,3,4,5的五个相同小球,随机放入编码分别为1,2,3,
4,5的五个小盒中,每盒仅放一球,若第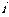 号小球恰好落入第
号小球恰好落入第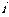 号小盒中,则称其
号小盒中,则称其
为一个匹对,用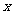 表示匹对的个数.
表示匹对的个数.
⑴ 求第3号小球恰好落入第3号小盒内的概率;
⑵ 求1号小球不落入1号盒子中,且5号小球不落入5号盒子中的 概率.
概率.
[来源:]
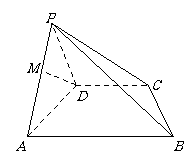
⒚(12分)如图,四棱锥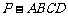 中,底面
中,底面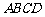 是直角梯形,
是直角梯形,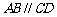 ,
,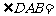
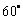 ,
,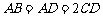 ,侧面
,侧面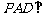 底面
底面 ,且
,且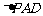 为等腰直角三角形,
为等腰直角三角形,
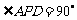 ,
,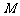 为
为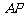 的中点.
的中点.
⑴ 求证: ;
;
⑵ 求二面角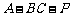 的余弦值.
的余弦值.
⒛ (12分)已知数列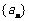 的首项为
的首项为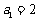 ,前
,前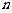 项和为
项和为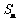 ,且对任意的
,且对任意的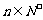 ,当
,当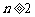
时,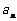 总是
总是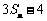 与
与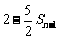 的等差中项.
的等差中项.
⑴ 求数列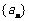 的通项公式;
的通项公式;
⑵ 设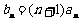 ,
,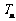 是数列
是数列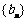 的前
的前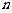 项和,
项和,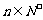 ,求
,求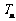 .
.
21.(1 2分)已知定义在
2分)已知定义在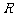 上的函数
上的函数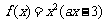 ,其中
,其中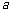 为常数.
为常数.
⑴ 若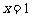 是函数
是函数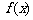 的一个极值点,求
的一个极值点,求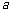 的值;
的值;
⑵ 若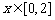 时,函数
时,函数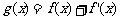 在
在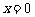 处取得最大值,求正数
处取得最大值,求正数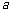 的取
的取
值范围.
⒔ 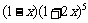 展开式按
展开式按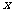 的升幂排列,则第3项的系数为 .
的升幂排列,则第3项的系数为 .
⒕ 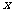 、
、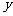 满足约束条件:
满足约束条件: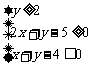 ,则
,则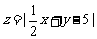 的最小值是
的最小值是  .
.
⒖ 已知两点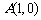 ,
,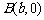 ,若抛物线
,若抛物线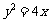 上存在点
上存在点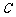 使
使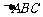 为等边三角形,
为等边三角形,
则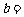 .
.
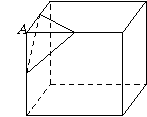 ⒗ 如图,设
⒗ 如图,设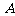 是棱长为
是棱长为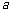 的正方体的一个顶点,过从此顶
的正方体的一个顶点,过从此顶
点出发的三条棱的中点作截面,对正方体的所有顶点都
如此操作,所得的各截面与正方体各面共同围成一 个多
个多
面体,则关于此多面体有以下结论:①
有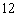 个顶点;
个顶点;
②
有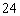 条棱;③ 有
条棱;③ 有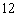 个面;④ 表面积为
个面;④ 表面积为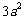 ;⑤ 体
;⑤ 体
积为
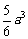 .其中正确的结论是
(要求填上所有正
.其中正确的结论是
(要求填上所有正
确结论的序号).
⒈ 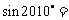
A.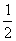 B.
B.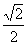 C.
C.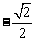 D.
D.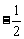
⒉ 设全集为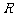 ,集合
,集合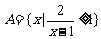 ,
,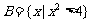 则
则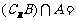
A.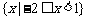 B.
B.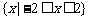 C.
C.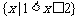 D.
D.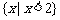 [来
[来
⒊ 在等差数列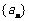 中,有
中,有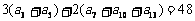 ,则此数列的前
,则此数列的前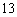 项和为
项和为
A.24 B.39 C.52 D.104
⒋ 若曲线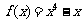 在点
在点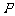 处的切线平行于直线
处的切线平行于直线
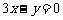 ,则点
,则点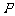 的坐标为
的坐标为
A.(1,3) B.(-1,3) C.(1,0) D.(-1,0)
⒌ 设偶函数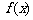 在
在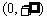 上为减函数,且
上为减函数,且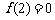 ,则不等式
,则不等式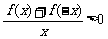 的
的
解集为
A.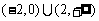 B
B .
.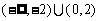 C.
C.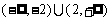 D.
D.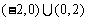
⒍ 设集合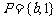 ,
,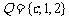 ,
,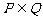 ,若
,若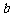 、
、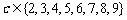 ,则
,则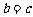 的
的
概率是
A.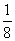 B.
B.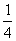 C.
C.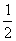
 D.
D.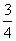
⒎ 已知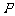 是边长为2的正
是边长为2的正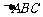 边
边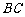 上的动点,则
上的动点,则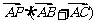 的值
的值
A.最大值为8  B.是定值6 C.最小值2 D.与
B.是定值6 C.最小值2 D.与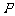 的位置有关
的位置有关
⒏ 将函数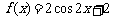 的图象按向量
的图象按向量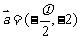 平移后得到的图象的函数为
平移后得到的图象的函数为
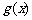 ,若函数
,若函数
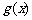 是奇函数,且在
是奇函数,且在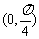 上是增函数,则
上是增函数,则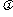 的一个值为
的一个值为
A.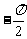 B.
B.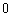 C.
C.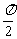 D.
D.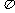
⒐ 已知四棱柱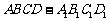 的底面为正方形,侧棱与底面边长相等,且点
的底面为正方形,侧棱与底面边长相等,且点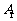 在底
在底
面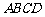 内的射影为正方形
内的射影为正方形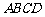 的中心,则
的中心,则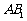 与底面
与底面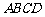 所成角的正弦值
所成角的正弦值
等于
A.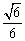 B.
B.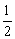
 C.
C.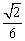 D.
D.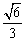
⒑ 已知函数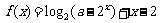 ,若
,若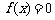 有解,则实数
有解,则实数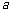 的取值范围是
的取值范围是
A.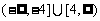 B.
B. C.
C.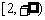 D.
D.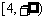
⒒ 已知椭圆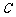 中,原点
中,原点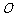 为中心,
为中心,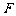 为左焦点,
为左焦点,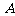 为左顶点,椭圆的左准线交
为左顶点,椭圆的左准线交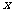 轴
轴
于点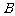 ,
,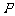 、
、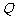 为椭圆上两动点,
为椭圆上两动点,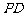 垂直左准线于点
垂直左准线于点 ,
,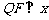 轴,则椭圆的
轴,则椭圆的
离心率为① 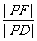 ;②
;② 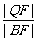 ;③
;③ 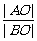 ;④
;④ 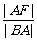 ;⑤
;⑤ 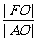 .
.
上述离心率正确的个数有
A.2个 B.3个 C.4个 D.5个
⒓ 将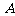 、
、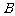 、
、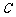 、
、 、
、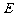 五种不同的文件放入一排编号依次为1,2,3,4,5,6的
五种不同的文件放入一排编号依次为1,2,3,4,5,6的
六个抽屉内,每个抽屉至多放一种文件,若文件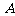 、
、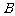 必须放入相邻的抽屉内,文
必须放入相邻的抽屉内,文
件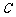 、
、 也必须放入相邻的抽屉内,则文件放入抽屉内的满足条件的所有不同的
也必须放入相邻的抽屉内,则文件放入抽屉内的满足条件的所有不同的
方法数为
A.144 B.80 C.48 D.96
18、有明显颜色变化的有机反应:
(1).苯酚与三氯化铁溶液反应呈紫色;
(2).KMnO4酸性溶液的褪色;
(3).溴水的褪色;
(4).淀粉遇碘单质变蓝色。
(5).蛋白质遇浓硝酸呈黄色(颜色反应)
17.能与NaOH溶液发生反应的有机物:
(1)酚:
(2)羧酸:
(3)卤代烃(水溶液:水解;醇溶液:消去)
(4)酯:(水解,不加热反应慢,加热反应快)
(5)蛋白质(水解)
16.既能与酸又能与碱反应的有机物:具有酸、碱双官能团的有机物(氨基酸、蛋白质等)
15.能使蛋白质变性的物质有:强酸、强碱、重金属盐、甲醛、苯酚、强氧化剂、浓的酒精、双氧水、碘酒、三氯乙酸等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com