
2.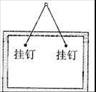 用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力为
用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力为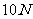 ,为使绳不断裂,画框上两个挂钉的间距最大为(
,为使绳不断裂,画框上两个挂钉的间距最大为(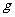 取
取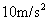 )
)
A.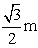 B.
B.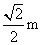 C.
C.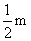 D.
D.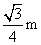
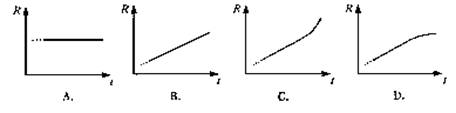
1. 大爆炸理论认为,我们的宇宙起源于137亿年前的一次大爆炸。除开始瞬间外,在演化至今的大部分时间内,宇宙基本上是半径匀速膨胀的。上世纪末,对1A型超新星的观测显示,宇宙正在加速膨胀,面对这个出人意料的发现,宇宙学家探究其背后的原因,提出宇宙的大部分可能由暗能量组成,它们的排斥作用导致宇宙在近段天文时期内开始加速膨胀。如果真是这样,则标志宇宙大小的宇宙半径R和宇宙年龄的关系,大致是下面哪个图像?
9. 解法一:
①设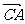 =
=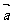 ,
,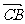 =
=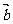 ,
, =
=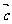
令 =λ
=λ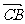 =λ
=λ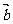 (λ≠0)
(λ≠0)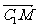 =
= -
- =λ
=λ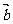 -
-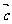
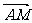 =
= -
-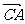 =λ
=λ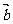 -
-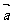
依题得: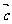 ·
·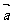 =0 ,
=0 ,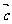 ·
·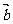 =0,
=0,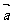 ·
·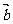 =1/2 a2
=1/2 a2
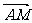 ·
· =(λ
=(λ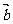 -
-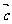 )·(λ
)·(λ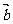 -
-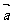 )=λ2
)=λ2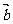 2-λ
2-λ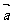
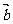 -λ
-λ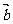
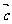 +
+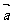
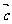
=λ2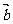 2-λ
2-λ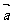
 =(λ2-λ/2)a2
=0
=(λ2-λ/2)a2
=0
所以λ=1/2 ,即点M为BC的中点
②设点H为点C在平面AMC1上的射影
令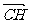 =
=  且x+y+z=1
且x+y+z=1
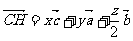 ,由
,由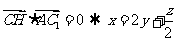 又由
又由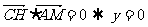
得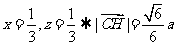 ,点C到平面AMC1的距离为
,点C到平面AMC1的距离为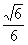 a
a
③平面AMG的法向量为
平面AC1C的法向量为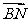 ,其中N为AC的中点
,其中N为AC的中点
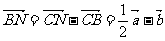 ,
, ,
,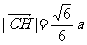 ,
,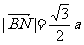
 则二面角M-AC1-C为45°
则二面角M-AC1-C为45°
解法二:
② ∵C1C⊥面ABC; C1M⊥AM 由三垂线定理的逆定理解CM⊥AM
∵△ABC为正三角形,AM为△ABC的中线,即点M为BC的中点
②利用等积法
Vc-AMC1=Vc1-AMC 可得C到平面AMC1的距离为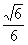 a
a
③过M作ME⊥AC,垂足为E,过E作EF⊥AC1交AC1于点F,连MF,则∠EFM为二面角M-AC1-C的平面角,易得∠EFM=45°
8.方案一:
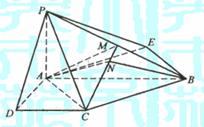 (Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连结AE,可知AC=CB=BE=AE=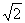 ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=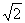 ,PB=
,PB=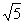 ,
, 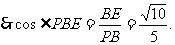

(Ⅲ)解:作AN⊥CM,垂足为N,连结BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角.
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC=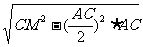 ,
,
 . ∴AB=2,
. ∴AB=2,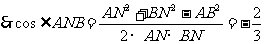
故所求的二面角为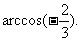
方法二:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为
A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,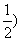 .
.
(Ⅰ)证明:因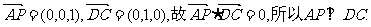
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD.
 (Ⅱ)解:因
(Ⅱ)解:因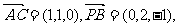
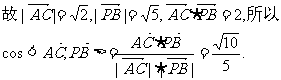
(Ⅲ)解:在MC上取一点N(x,y,z),则存在
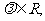 使
使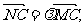
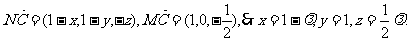
要使

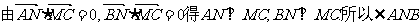 为所求二面角的平面角.
为所求二面角的平面角.

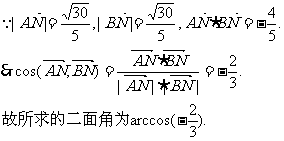
7.方法一:①∵M、N分别是点AB、PC的中点,可得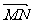 =1/2 (
=1/2 (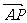 +
+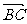 )由于
)由于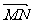 ·
·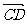 =1/2(
=1/2(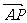 +
+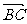 )·
)·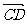 =1/2(
=1/2(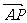 ·
·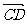 +
+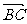 ·
·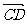 )=0
)=0
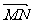 ·
·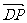 =1/2 (
=1/2 (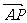 +
+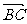 )·(
)·(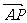 -
-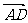 )=1/2(
)=1/2(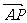 +
+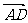 )(
)(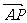 -
-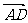 )=0
)=0
∴MN⊥CD MN⊥DP ∴MN⊥平面PCD =>平面MND⊥平面PCD
②∵底面的法向量为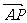 ,得平面MND的法向量为
,得平面MND的法向量为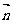 =λ
=λ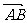 +μ
+μ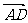 +
+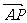
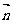 ·
·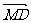 =(λ
=(λ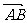 +μ
+μ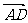 +
+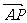 )·(
)·(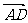 -
-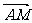 )= -λ
)= -λ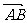 ·
·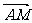 +μ
+μ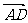 ·
·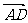 = -a2+μa2=0 ∴λ=μ
= -a2+μa2=0 ∴λ=μ
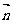 ·
·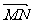 =(λ
=(λ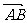 +μ
+μ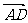 +
+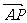 )·1/2 (
)·1/2 (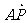 +
+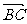 )=1/2 (|
)=1/2 (|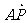 |2+λ
|2+λ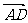 ·
·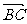 )=1/2 (a2+λa2)=0 ∴λ=M= -1
)=1/2 (a2+λa2)=0 ∴λ=M= -1
∴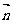 = -
= -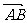 -
-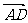 +
+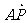 cosθ=
cosθ= 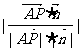 =
=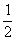 ∴二面角N-MD-C为60
∴二面角N-MD-C为60
解法二:①连PM、MC 易得PM=MC 又N为PC的中点,∴MN⊥PC
取DC的中点为Q。连MQ ,NQ 则NQ//PD MQ//AD
∵PA⊥面ABCD,又DA⊥CD 由三垂线定理的逆定理得PD⊥CD
∴NQ⊥CD,MQ⊥CD ∴CD⊥面MNQ ∴CD⊥MN
∴MN⊥平面PCD ,MN  面MND
∴平面MND⊥平面PCD。
面MND
∴平面MND⊥平面PCD。
①连AC取AC的中点O,则NO⊥平面ABCD
过O作OE⊥DM 连NE 由三垂线定得得NE⊥DM
∴∠NEO为二面角N-MD-C的平面角
其中NO=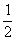 PA=
PA=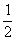 a; AC=
a; AC=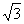 a DM=
a DM= 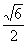 a
a
OE=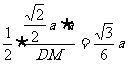 tan∠NEO=
tan∠NEO= 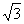
∴∠NEO=60°,即二面角N-MD-C为60°
1、C 2 、A 3、 C 4、B 5、A 6、
9、如图,正三棱柱ABC-A1B1C1的底长为a,点M在边BC上,△AMC1是以点M为直
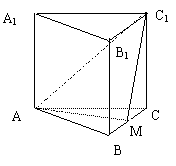 角顶点的等腰直角三角形:
角顶点的等腰直角三角形:
①求证:点M为边BC的中点
②求点C到平面AMC1的距离
③求二面角M-AC1-C的大小
第23讲 空间角与距离(2)
[课前热身]1、C 2、A 3、B 4、30 度5、18π
[例题探究]
例1: (I)证明:∵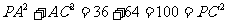
∴△PAC是以∠PAC为直角的直角三角形,同理可证
 △PAB是以∠PAB为直角的直角三角形,△PCB是以∠PCB为直角的直角三角形。
△PAB是以∠PAB为直角的直角三角形,△PCB是以∠PCB为直角的直角三角形。
故PA⊥平面ABC
又∵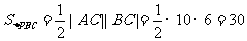
而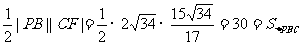
故CF⊥PB,又已知EF⊥PB
∴PB⊥平面CEF
(II)由(I)知PB⊥CE, PA⊥平面ABC
∴AB是PB在平面ABC上的射影,故AB⊥CE
在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,
EF1是EF在平面ABC上的射影,∴EF⊥EC
故∠FEB是二面角B-CE-F的平面角。
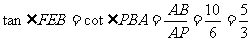
二面角B-CE-F的大小为
例2.解法一:(1)∠PMD为二面角P-MN-D的平面角。…………4分
计算得二面角P-MN-D的大小为120°。…………8分
(2)①若∠CDN=90°,与题意不符………………10分
②若∠DCN=90°,可算得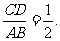 …………12分
…………12分
③若∠DNC=90°,可算得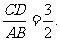 …………15分
…………15分
解法二:用向量方法(略)
例3:(1)当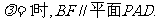
证明:取PD中点E,则EF//CD,且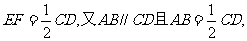
∴四边形ABFE为平行四边形.
∴BF//AE. 又AE 平面PAD ∴BF//平面PAD
平面PAD ∴BF//平面PAD
(2)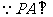 平面ABCD,
平面ABCD,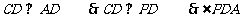 即是二面角的平
即是二面角的平
面角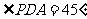
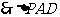 为等腰直角三角形,
为等腰直角三角形,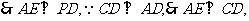
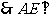 平面PCD 又BF//AE,
平面PCD 又BF//AE,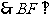 平面PCD.
平面PCD. 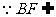 平面PBC,
平面PBC,
∴平面PCD⊥平面PBC,即二面角B-PC-D的大小为90°.
(3)在平面PCD内作EH⊥PC于点H,由平面PCD⊥平面PBC且平面PCD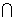
平面PBC=PC知:EH⊥平面PBC.
在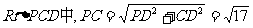 ,
,
在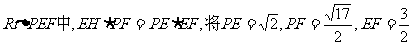 代入得:
代入得:
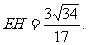 即点E到平面PBC的距离为
即点E到平面PBC的距离为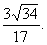
又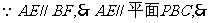 点A到平面PBC的距离为
点A到平面PBC的距离为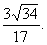
[冲刺强化训练23]
8、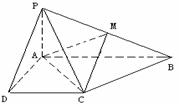 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
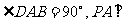 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=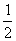 AB=1,
AB=1,
M是PB的中点。
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小。
7、如图,PA 矩形ABCD所在平面,PA=AD=a, M、N分别是AB、PC的中点,
矩形ABCD所在平面,PA=AD=a, M、N分别是AB、PC的中点,
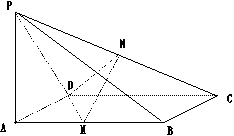 (1)证明平面MND
(1)证明平面MND 平面PCD;
平面PCD;
(2)若AB= ,求二面角N-MD-C的大小。
,求二面角N-MD-C的大小。
6、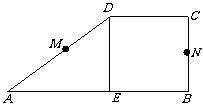 设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于______.
设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com