
1.36 2.A 3.C 4.B 5.1440 6.C
1.C 2.A 3.21 4.C 5.76542
[例题探究]
例1.(1)第一节排数学时,共有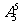 种排法,第一节不排数学时,有
种排法,第一节不排数学时,有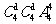 种排法,故所有的排法共有
种排法,故所有的排法共有 种。
种。
另解:所有的排法共有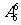 种,体育排在第一节的排法有
种,体育排在第一节的排法有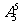 种,数学排在最后一节的排法有
种,数学排在最后一节的排法有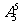 种,体育排在第一节且数学排在最后一节的排法有
种,体育排在第一节且数学排在最后一节的排法有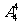 种,故满足条件的所有的排法共有
种,故满足条件的所有的排法共有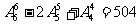 种。
种。
(2) 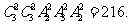
[教学建议]引导学生从不同的角度来处理问题。
例2.(1)每个球均有4种不同的放法,故所有的放法有4·4·4·4=256种,(2)恰有一个盒子不放球,也即有一个盒子放两个球,另两个盒子各放一个球的放法有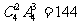 种,(3)恰有一个盒子放两个球,也即有一个盒子不放球,另两个盒子各放一个球的放法有
种,(3)恰有一个盒子放两个球,也即有一个盒子不放球,另两个盒子各放一个球的放法有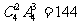 种,(4)分两类,一类是一个盒子放3个球,另一个盒子放1个球,共
种,(4)分两类,一类是一个盒子放3个球,另一个盒子放1个球,共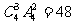 种放法,另一类是两个盒子均放两个球,共有
种放法,另一类是两个盒子均放两个球,共有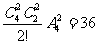 种放法,故所有的不同放法共有
种放法,故所有的不同放法共有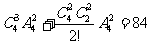 种。
种。
例3.先选3种颜色的花分别栽种在区域1、2、3上,然后对区域5与区域2、3的颜色是否相同进行讨论:(1)区域5与区域2相同,区域4 只有一种栽法,区域6有2种栽法,共有4·3·2·1·1·2=48种不同的栽法;(2)区域5与区域3相同,区域6 只有一种栽法,区域4有2种栽法,共有4·3·2·1·1·2=48种不同的栽法;(3)区域5与区域2、3均不相同,共有4·3·2·1·1·1=24种不同的栽法;故所有不同的栽种方法共有48+48+24=120种。
备用题.(1)解:
(2)解: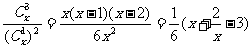
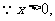

(3)解:性质①不能推广。例如当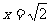 时,
时,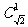 有意义,但
有意义,但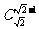 无意义;
无意义;
性质②能推广,它的推广形式是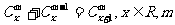 是正整数。事实上,
是正整数。事实上,
当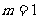 时,有
时,有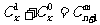 ;
;
当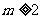 时,
时,
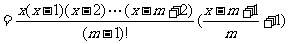
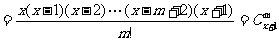
冲刺强化训练(24)
9、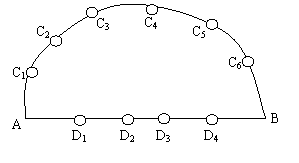 如图,以AB为直径的半圆周上有异于A、B的6个点
如图,以AB为直径的半圆周上有异于A、B的6个点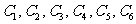 。线段AB上有异于A、B的4个点
。线段AB上有异于A、B的4个点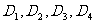 。问:(1)以这10 个点(不包括A、B)中的3个点为顶点可作几个三角形?其中含点
。问:(1)以这10 个点(不包括A、B)中的3个点为顶点可作几个三角形?其中含点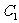 的三角形有几个?(2)以图中的12个点中的4 个点为顶点可作多少个四边形?
的三角形有几个?(2)以图中的12个点中的4 个点为顶点可作多少个四边形?
第24讲 排列、组合应用题
[课前热身]
8、将1,2,3,4,5,6,7,8,9这九个数字填入右图的空格中,要求每行从左到右,每列从上到下都依次增大,且4已经固定,求所有不同的填入方法数。
|
|
|
|
|
|
4 |
|
|
|
|
|
7、设坐标平面内有一个质点从原点出发,沿x轴方向跳动,每次向正方向或负方向跳1个单位,经过7次跳动质点落在点(3,0)(允许重复过此点)处,求质点不同的运动方法种数(用数字作答)。
6、若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y= -x2,值域为{-1,-9}的“同族函数”共有 ( )
A.7个 B.8个 C.9个 D.10个
5、为配制某种染色剂, 需要加入三种有机染料、两种无机染料和两种添加剂, 其中有机染料的添加顺序不能相邻.现要研究所有不同添加顺序对染色效果的影响, 总共要进行的试验次数为 .(用数字作答)
4、设{an}为等差数列,从{a1,a2,a3,···a10}中任取3个不同的数,使这三个数仍成等差数列,则这样的等差数列最多有( )
(A)90个 (B)120个 (C)180个 (D)200个
3、如图,在一个田字形区域A、B、C、D中栽种观赏植物,
要求同一区域中种同一种植物.相邻两区域中种不同的植物
(A与D、B与C不为相邻)现 有4种不同的植物可供选择,则
不同的种植方案有 ( )
(A)24种 (B)36种 (C) 48种 (D) 84种
2、6名运动员站在6条跑道上准备参加比赛,其中甲不能站在第一道也不能站在第二道,乙必须站在第五道或第六道,则不同排法种数共有( )
(A) 144 (B) 96 (C) 72 (D) 48
|
A |
B |
|
C |
D |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com