
7. 三垂线定理要注意“平面内”的条件:“平面内”一条直线垂直于“射影”则垂直于斜线。由三垂线定理得到的两个常用结论:①直线与角的两边所成的角相等,则直线在(角所在的)平面内的射影是角的平分线;②直线与平面内一条直线所成角的余弦等于直线与它在平面内的射影所成角的余弦和射影与这条直线所成角的余弦的积。
[举例]在平行六面体ABCD-A1B1C1D1,已知AB=AD=4,,AA1=3, ∠A1AB=∠A1AD=
∠BAD=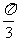 ,(1)求AC1的长(2)求平行六面体ABCD-A1B1C1D1的体积。
,(1)求AC1的长(2)求平行六面体ABCD-A1B1C1D1的体积。
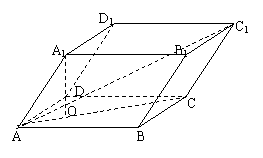 解析:记A1在面ABCD内的射影为O,
解析:记A1在面ABCD内的射影为O,
∵∠A1AB=∠A1AD,∴O在∠BAD的平分线上,
又AB=AD,∴∠BAD的平分线即菱形ABCD的
对角线AC,故O在AC上;
∵cos∠A1AB=cos∠A1AO×cos∠OAB
∴cos∠A1AO=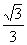 ,∴sin∠A1AO=
,∴sin∠A1AO= ,
,
cos∠ACC1=-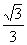 ;又AC=4
;又AC=4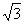 ,在⊿ACC1中由余弦定理得AC1=9;在⊿A1AO中,A1O=
,在⊿ACC1中由余弦定理得AC1=9;在⊿A1AO中,A1O=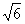 ,
,
 =
=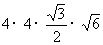 =24
=24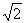 。
。
注:求AC1的长还可以用向量: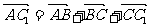 ,平方即可。
,平方即可。
[巩固]MN是两条互相垂直的异面直线a、b的公垂线段,点P是线段MN上除M,N外一动点,若点A是a上不同于公垂线垂足的一点,点B是b上不同于公垂线垂足的一点,△APB是:A、锐角三角形 B、钝角三角形 C、直角三角形 D、以上均有可能
6.已知“面面垂直”的条件,一般发展为“一个面内垂直于交线的直线垂直于另一个面”。在直棱柱中隐藏着侧面与底面垂直的条件。
[举例] 四棱锥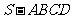 中,底面
中,底面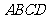 为平行四边形,侧面
为平行四边形,侧面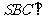 底面
底面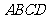 .已知
.已知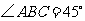 ,
,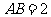 ,
,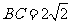 ,
,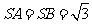 .证明:
.证明: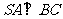 ;
;
(07高考全国卷Ⅰ理19)
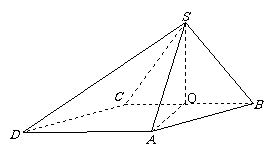 解析:作
解析:作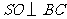 ,垂足为
,垂足为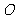 ,连结
,连结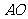 ,
,
由侧面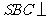 底面
底面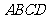 ,得
,得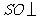 底面
底面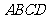 .
.
∵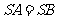 ,∴
,∴ 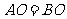 ,又
,又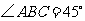
故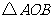 为等腰直角三角形,
为等腰直角三角形,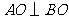 ,
,
又SO⊥BO,∴BC⊥面SAO,∴BC⊥SA
(或直接由三垂线定理得到).
 注:证明“线线垂直”一般去证一条“线”垂直于
注:证明“线线垂直”一般去证一条“线”垂直于
过另一条“线”的面,或者使用三垂线定理。
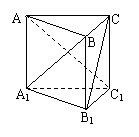
[巩固] 如图,已知直三棱柱ABC-A1B1C1中,B1C1= A1C1,
A1B⊥AC1,求证:A1B⊥B1C。
6. 证明“面面垂直”关键要找准哪个平面内的哪条直线垂直于另一个平面. 也可以证明两个平面的法向量垂直
证明“面面垂直”关键要找准哪个平面内的哪条直线垂直于另一个平面. 也可以证明两个平面的法向量垂直
 [举例] 如图,已知PA⊥矩形ABCD所在的平面,
[举例] 如图,已知PA⊥矩形ABCD所在的平面,
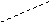 M、N分别是AB,PC的中点;若P-CD-A为450
M、N分别是AB,PC的中点;若P-CD-A为450
 的二面角,求证: 平面MND⊥平面PDC;
的二面角,求证: 平面MND⊥平面PDC;
解析:仅仅观察平面MND和平面PDC,很难
发现垂直的线索;从二面角P-CD-A入手,易见
CD⊥AD,CD⊥AP,∴CD⊥面PAD,∴CD⊥PD,即
∠PDA是二面角P-CD-A的平面角,∴∠PDA=450,那么在Rt⊿PAD中有AP=AD,取PD中点E,则AE⊥PD,又由CD⊥面PAD得CD⊥AE,故AE⊥面PCD;而EN平行且等于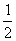 DC,即EN平行且等于AM,∴四边形AMNE是平行四边形,即MN∥AE;于是有MN⊥面PCD,
DC,即EN平行且等于AM,∴四边形AMNE是平行四边形,即MN∥AE;于是有MN⊥面PCD,
 又∵MN在面MND内,∴平面MND⊥平面PDC。
又∵MN在面MND内,∴平面MND⊥平面PDC。
[巩固]如图,直三棱柱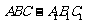 中,
中,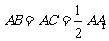 ,
,
 ,
,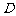 为棱
为棱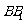 的中点.
的中点.
求证:平面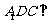 平面
平面 .
.
5.已知“线面平行”的条件,一般只有一个“发展”方向:过“线”的议和平面与已知“面”的交线和已知的“线”平行,故设法找到经过“线”的平面与已知“面”的交线往往是解题的关键。
[举例]如图4-1,正四棱锥S-ABCD的底面边长为a,侧棱长为2a,点P、Q分别在BD和SC上,并且BP:PD=1:2,PQ∥面SAD,求线段PQ的长。
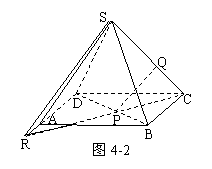
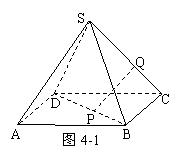
解析:要用条件“PQ∥面SAD”,需找到过PQ的平面与面SAD的交线,方法有二:①分别延长CP、DA交于点R,如图4-2,则面SCR交面SAD于SR,又PQ∥面SAD,∴QP∥SR;
而在面ABCD中,⊿PDR∽⊿PBC,且PD=2PB,∴PR=2PC,PR=2BC=2a; 于是在⊿CSR中有:SR=3QP;在等腰⊿SAD中,可以求出cos∠SDA=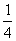 ,则在⊿SRD中由余弦定理可以求得SR=
,则在⊿SRD中由余弦定理可以求得SR=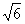 a,即PQ=
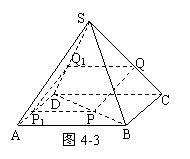
a,即PQ= a;②过P、Q分别作CD的平行线,分别交AD于P1、交SD于Q1,连P1Q1,如图4-3,面PP1Q1Q交面SAD于P1Q1且PQ∥面SAD,则PQ∥P1Q1,∴四边形PP1Q1Q是平行四边形,即PQ=P1Q1;在⊿DAB中,∵PD=2PB,∴PD=2PA=
a;②过P、Q分别作CD的平行线,分别交AD于P1、交SD于Q1,连P1Q1,如图4-3,面PP1Q1Q交面SAD于P1Q1且PQ∥面SAD,则PQ∥P1Q1,∴四边形PP1Q1Q是平行四边形,即PQ=P1Q1;在⊿DAB中,∵PD=2PB,∴PD=2PA=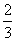 a,PP1=
a,PP1=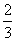 AB=
AB=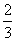 a,
a,
 ∴QQ1=
∴QQ1=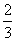 a=
a=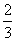 CD,于是在⊿SCD中有:SQ1=
CD,于是在⊿SCD中有:SQ1=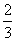 SD,
SD,
∴Q1D=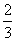 a,仿方法①可以求出P1Q1。
a,仿方法①可以求出P1Q1。
[巩固]如图,在矩形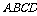 中,
中,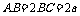 ,
,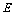 为
为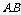
上一点,将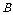 点沿线段
点沿线段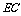 折起至点
折起至点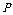 ,连结
,连结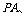
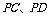 ,
,
取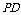 的中点
的中点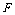 ,若有
,若有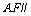 平面
平面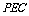 .试确定
.试确定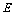 点位置。
点位置。
4.证明“线面平行”的关键是找准“这条直线”平行于平面内的哪条直线,(也可以先证经过“这条直线”的平面与平面平行);
[举例] 右图是一个直三棱柱(以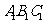 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为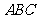 .已知
.已知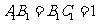 ,
,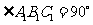 ,
,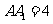 ,
,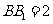 ,
,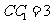 .
.
 若点
若点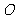 是
是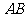 的中点,证明:
的中点,证明: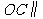 平面
平面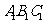 ;(07高考江西理20)
;(07高考江西理20)
解析:取A1B1中点 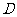 ,连
,连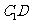 .则
.则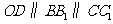 .
.
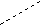
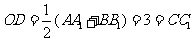 .
.
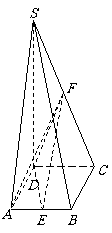 ∴四边形
∴四边形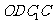 是平行四边形,因此有
是平行四边形,因此有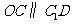 .
.
又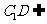 平面
平面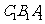 且
且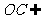 平面
平面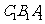 ,∴
,∴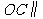 面
面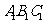 .
.
注:在找“线”与面内的一条直线平行时,常用到一些平面图形的性质,
如:三角形的中位线、梯形中位线、平行四边形、平行线分线段成比例
定理的逆定理等。
[巩固] 如图,在四棱锥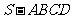 中,底面
中,底面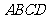 为正方形,
为正方形,
侧棱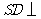 底面
底面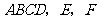 分别为
分别为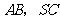 的中点.
的中点.
证明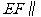 平面
平面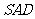 ;(07高考全国卷Ⅱ理19)
;(07高考全国卷Ⅱ理19)
3.证明立几问题时要有降维的思想:通过线线垂直证线面垂直,通过线面垂直证面面垂直;通过线线平行证线面平行,通过线面平行证面面平行。
2.在分析比较复杂的“孤立”的线面关系(不在几何体中)时,可以将其放置于一个我们熟悉的几何体(如三棱锥、长方体等)中研究,以便观察、寻找它们之间的联系。
[举例] 设 为平面,
为平面, 为直线,以下四组条件:①
为直线,以下四组条件:① 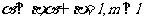 ②
②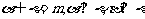 ; ③
; ③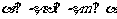 ;④
;④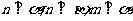 ;可以作为
;可以作为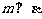 的一个充分条件是
。
的一个充分条件是
。
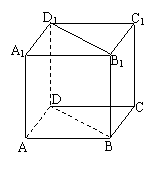 解析:题中线面关系既复杂又抽象,注意到其中包含大量的垂直关系,故可以在正方体内观察:①记面AD1为
解析:题中线面关系既复杂又抽象,注意到其中包含大量的垂直关系,故可以在正方体内观察:①记面AD1为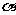 ,面AC为
,面AC为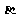 ,则AD为
,则AD为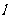 ,若视AB为
,若视AB为
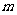 ,
,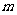 ⊥
⊥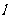 ,但
,但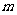 在面
在面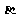 内;②若
内;②若 两两垂直,则
两两垂直,则
可以得到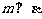 ,但该条件中没有
,但该条件中没有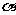 ⊥
⊥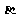 ,故反例只可能存在
,故反例只可能存在
于此处,记面AD1为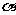 ,面BB1D1D为
,面BB1D1D为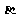 ,面AC为
,面AC为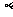 ,则AD
,则AD
为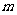 ,但
,但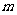 与
与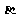 成450角;③注意到
成450角;③注意到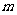 ⊥
⊥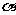 ,只要
,只要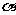 、
、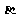 不平行,就得不到
不平行,就得不到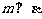 ,记面AD1为
,记面AD1为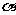 ,面BB1D1D为
,面BB1D1D为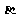 ,面AC为
,面AC为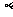 ,视AB为
,视AB为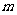 ,但
,但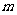 与
与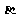 成450角;④由
成450角;④由
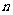 ⊥
⊥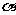 ,
,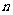 ⊥
⊥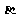 得
得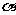 ∥
∥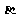 ,再由
,再由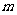 ⊥
⊥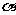 得
得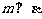 ;故只有④。
;故只有④。
[巩固]设 、
、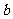 为直线,
为直线,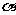 为平面,直线
为平面,直线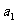 、
、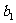 分别为
分别为 、
、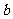 在面
在面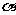 内的射影,则下列四个命题中正确的个数是:
( )
内的射影,则下列四个命题中正确的个数是:
( )
①若 ⊥
⊥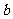 则
则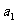 ⊥
⊥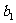 ;②若
;②若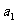 ⊥
⊥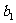 则
则 ⊥
⊥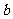 ;③若
;③若 ∥
∥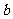 则
则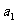 ∥
∥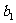 ;④若
;④若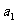 ∥
∥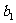 则
则 ∥
∥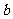
A.3, B.2 C.1, D.0
注:07年高考上海卷理科第10题就是由这一题变形、延伸而来:
[延伸]
在平面上,两条直线的位置关系有相交、平行、重合三种. 已知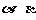 是两个 相交平面,空间两条直线
是两个 相交平面,空间两条直线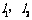 在
在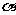 上的射影是直线
上的射影是直线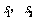 ,
,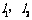 在
在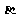 上的射影是直线
上的射影是直线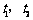 .用
.用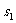 与
与 ,
,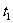 与
与 的位置关系,写出一个总能确定
的位置关系,写出一个总能确定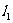 与
与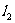 是异面直线的充分条件:
是异面直线的充分条件:
1.“公理1”用于证明“线在面内”;“公理2”用于证明“点在线上”,“公理3”及其推论用于证明“共面”。
[举例1]⊿ABC和⊿A1B1C1所在的平面交于直线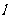 ,AB和A1B1交于P,BC和B1C1交于Q,AC和
,AB和A1B1交于P,BC和B1C1交于Q,AC和
A1C1交于R,则下列判断正确的是: ( )
A.P、Q、R确定平面 ,且
,且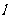

 ; B.P、Q、R确定平面
; B.P、Q、R确定平面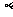 ,且
,且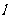 ∥
∥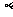 ;
;
C.P、Q、R确定平面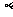 ,且
,且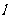 ⊥
⊥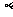 ;
D.P、Q、R都在直线
;
D.P、Q、R都在直线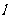 上
上
 解析:易见P是平面ABC和平面A1B1C1的一个公共点,由公理2知,P在它们的公共线
解析:易见P是平面ABC和平面A1B1C1的一个公共点,由公理2知,P在它们的公共线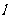 上,
上,
同理:Q、R也在直线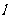 上。
上。
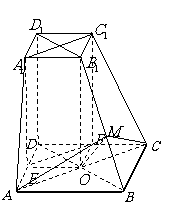
[举例2] 如图,在六面体 中,
中,
四边形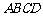 是边长为2的正方形,四边形
是边长为2的正方形,四边形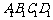
是边长为1的正方形,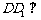 平面
平面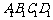 ,
,
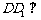 平面
平面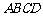 ,
, .
.
求证: 与
与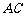 共面,
共面,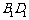 与
与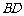 共面.
共面.
(07高考安徽理17)
解析:几何体为六面体,则AB、A1B1共面,BC、B1C1共面,
CD、C1D1共面,AD、A1D1共面;
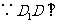 平面
平面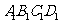 ,
,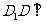 平面
平面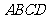 .
.
 ∴平面
∴平面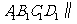 平面
平面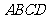
于是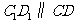 ,
,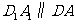 .
.
设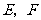 分别为
分别为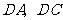 的中点,连结
的中点,连结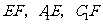 ,
,
有:A1D1平行且等于AD,故A1E平行且等于DD1,
同理C1F平行且等于DD1,于是A1E平行且等于C1F
∴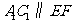 .又由
.又由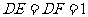 ,得
,得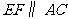 ,
,
故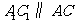 ,
,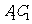 与
与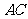 共面.过点
共面.过点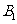 作
作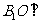 平面
平面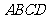 于点
于点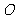 ,则
,则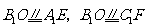 ,连结
,连结 ,于是
,于是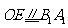 ,
,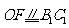 ,
,
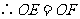 .
.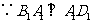 ,
,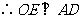 .
.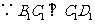 ,
,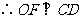 .
.
所以点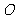 在
在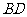 上,而
上,而 与DO共面,故
与DO共面,故 与
与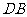 共面.
共面.
[巩固1]已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是: ( )
A.两两异面 B.两两平行 C.交于一点 D.两两相交。
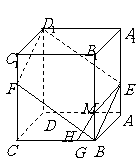 [巩固2] 如图,已知
[巩固2] 如图,已知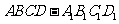 是棱长为
是棱长为 的正方体,
的正方体,
点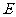 在
在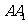 上,点
上,点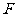 在
在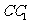 上,且
上,且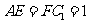 .
.
求证: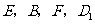 四点共面;
四点共面;
(07高考江苏卷18)
23.请根据下面的两幅图,介绍“海心塔”所在的位置,并描述“海心塔”塔身的形状特点。要求:连标点符号不超过60字。(6分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com