
7.(1)a= 利用定义证明(略):
利用定义证明(略):
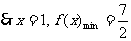









1. A 2. A 3.C 4.C
5.D
6. 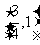
3.(1)由已知得 (1)即
(1)即

(2)要证原不等式成立.即证: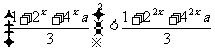
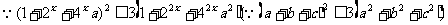
又0<a<1 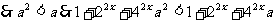

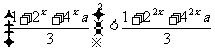 即
即 
冲刺强化训练(8)
2.(1)设乙车行驶t小时到D,甲车行驶t小时到E
① 若 ,则
,则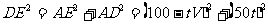 ,
,
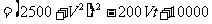 .当t=
.当t=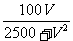 时,DE取最小值,其最小值为
时,DE取最小值,其最小值为
②若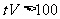 时,乙车停止,甲车继续前进,DE越来越大,无最小值
时,乙车停止,甲车继续前进,DE越来越大,无最小值
综上:甲,乙两车的最近距离为 千米
千米
(2)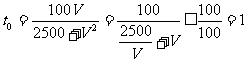 .当且仅当
.当且仅当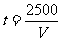 即t=50千米/小时时,
即t=50千米/小时时, 最大
最大
1. (1)由已知得: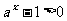
①当a>1时,x>0,则图象在y轴右侧
②当0<a<1时,x<0,则图象在y轴左侧;
(2)令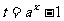 ,则
,则
①当a>1时,t在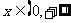 上递增,又
上递增,又 递增,
递增,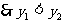
②当0<a<1时,t在 上递减,又
上递减,又 递减
递减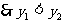
综上: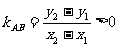
(3)由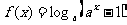 得
得
由 得
得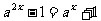

 函数
函数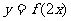 与图象
与图象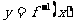 的交点坐标为
的交点坐标为
1. C 2. C 3.
D 4. a= -1或 a=-  5.
24
5.
24
9.设函数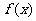 的定义域为D,若存在
的定义域为D,若存在 ,使
,使 成立,则称以
成立,则称以 为坐标的点为函数
为坐标的点为函数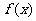 图象上的不动点.
图象上的不动点.
(1)
若函数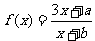 图象上有两个关于原点对称的不动点,求a,b应满足的条件;
图象上有两个关于原点对称的不动点,求a,b应满足的条件;
(2)
在(1)的条件下,若a=8,记函数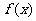 图象上的两个不动点分别为A,B,M为函数图象上的另一点,且其纵坐标
图象上的两个不动点分别为A,B,M为函数图象上的另一点,且其纵坐标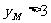 ,求点M到直线AB距离的最小值及取得最小值时M点的坐标;
,求点M到直线AB距离的最小值及取得最小值时M点的坐标;
(3)
下述命题“若定义在R上的奇函数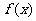 图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举一反例说明.
图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举一反例说明.
第8讲 函数的综合应用
8.过点M(-1,0)的直线 与抛物线
与抛物线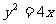 交于
交于 两点.记线段
两点.记线段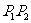 的中点为P,过点P和抛物线的焦点F的直线为
的中点为P,过点P和抛物线的焦点F的直线为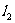 ;
; 的斜率为k,试把直线
的斜率为k,试把直线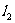 的斜率与直线
的斜率与直线 的斜率之比表示为k的函数,并指出这个函数的定义域,单调区间,同时说明在每单调区间上它是增函数还是减函数.
的斜率之比表示为k的函数,并指出这个函数的定义域,单调区间,同时说明在每单调区间上它是增函数还是减函数.
7.已知函数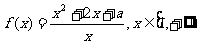
(1)
当 时,求函数
时,求函数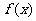 的最小值;
的最小值;
(2)
若对任意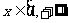 ,
,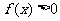 恒成立,试求实数a的取值范围.
恒成立,试求实数a的取值范围.
6.若函数 在区间
在区间 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com