
21. 如何解抽象函数问题?
(赋值法、结构变换法)
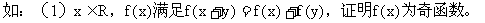
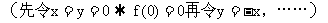
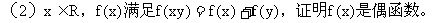

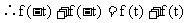
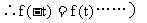
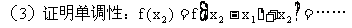
(对于这种抽象函数的题目,其实简单得都可以直接用死记了
20. 你在基本运算上常出现错误吗?
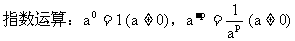
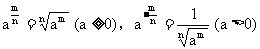
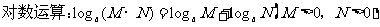
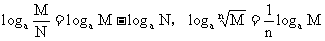
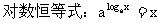
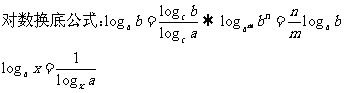
19. 你熟练掌握常用函数的图象和性质了吗?
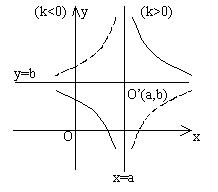
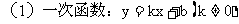 (k为斜率,b为直线与y轴的交点)
(k为斜率,b为直线与y轴的交点)
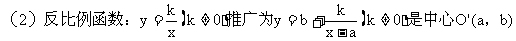
的双曲线。

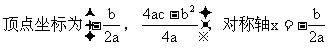
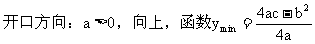
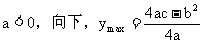


应用:①“三个二次”(二次函数、二次方程、二次不等式)的关系--二次方程
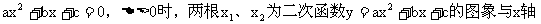
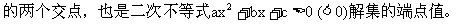
②求闭区间[m,n]上的最值。

③求区间定(动),对称轴动(定)的最值问题。
④一元二次方程根的分布问题。

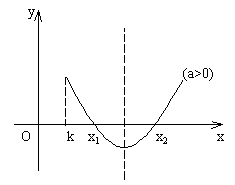
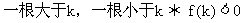

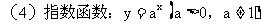
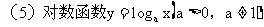
由图象记性质! (注意底数的限定!)
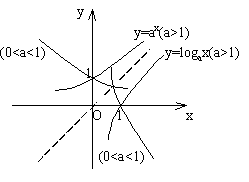

利用它的单调性求最值与利用均值不等式求最值的区别是什么?(均值不等式一定要注意等号成立的条件)
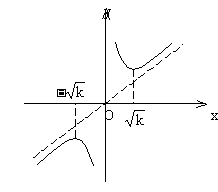
19. 你掌握常用的图象变换了吗?
 联想点(x,y),(-x,y)
联想点(x,y),(-x,y)
 联想点(x,y),(x,-y)
联想点(x,y),(x,-y)
 联想点(x,y),(-x,-y)
联想点(x,y),(-x,-y)
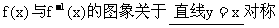 联想点(x,y),(y,x)
联想点(x,y),(y,x)
 联想点(x,y),(2a-x,y)
联想点(x,y),(2a-x,y)
 联想点(x,y),(2a-x,0)
联想点(x,y),(2a-x,0)
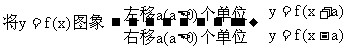

(这是书上的方法,虽然我从来不用, 但可能大家接触最多,我还是写出来吧。对于这种题目,其实根本不用这么麻烦。你要判断函数y-b=f(x+a)怎么由y=f(x)得到,可以直接令y-b=0,x+a=0,画出点的坐标。 看点和原点的关系,就可以很直观的看出函数平移的轨迹了。)
注意如下“翻折”变换:

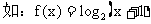

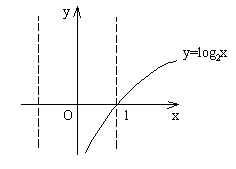
|
f(g) |
g(x) |
f[g(x)] |
f(x)+g(x) |
f(x)*g(x) |
|
奇 |
奇 |
奇 |
奇 |
偶 |
|
奇 |
偶 |
偶 |
非奇非偶 |
奇 |
|
偶 |
奇 |
偶 |
非奇非偶 |
奇 |
|
偶 |
偶 |
偶 |
偶 |
偶 |
18. 你熟悉周期函数的定义吗?
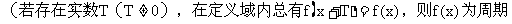
函数,T是一个周期。)
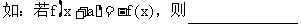
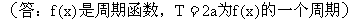
我们在做题的时候,经常会遇到这样的情况:告诉你f(x)+f(x+t)=0,我们要马上反应过来,这时说这个函数周期2t. 推导: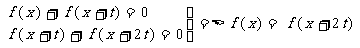 ,
,
同时可能也会遇到这种样子:f(x)=f(2a-x),或者说f(a-x)=f(a+x).其实这都是说同样一个意思:函数f(x)关于直线对称, 对称轴可以由括号内的2个数字相加再除以2得到。比如,f(x)=f(2a-x),或者说f(a-x)=f(a+x)就都表示函数关于直线x=a对称。

如:
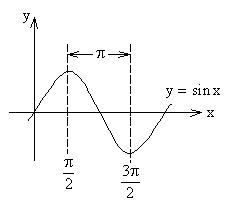
在给定函数的定义域关于原点对称的前提下,计算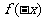 ,然后根据函数的奇偶性的定义判断其奇偶性.
,然后根据函数的奇偶性的定义判断其奇偶性.

一个函数是奇(偶)函数,其定义域必关于原点对称,它是函数为奇(偶)函数的必要条件.若函数的定义域不关于原点对称,则函数为非奇非偶函数.
.
22.已知函数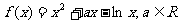 ;
;
(1)若函数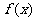 在
在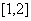 上是减函数,求实数
上是减函数,求实数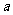 的取值范围;
的取值范围;
(2)令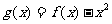 ,是否存在实数
,是否存在实数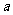 ,当
,当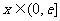 (
(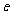 是自然常数)时,函数
是自然常数)时,函数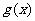 的最小值是
的最小值是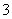 ,若存在,求出
,若存在,求出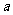 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)当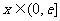 时,证明
时,证明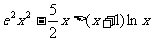
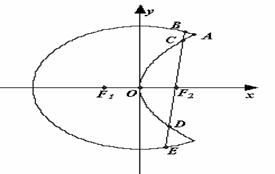
21.如图,曲线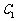 是以原点O为中心、
是以原点O为中心、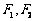 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线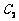 是以O为顶点、
是以O为顶点、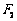 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线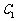 和
和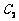 的交点且
的交点且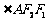 为钝角,若
为钝角,若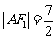 ,
,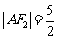 ,
,
 (1)求曲线
(1)求曲线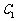 和
和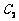 的方程;
的方程;
(2)过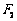 作一条与
作一条与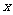 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线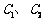 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,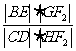 是否为定值?若是求出定值;若不是说明理由。
是否为定值?若是求出定值;若不是说明理由。
20. 某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品中至少有一种是日用商品的概率;
(2)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为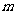 的奖金.假设顾客每次抽奖时获奖与否的概率都是
的奖金.假设顾客每次抽奖时获奖与否的概率都是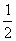 ,请问:商场应将每次中奖奖金数额
,请问:商场应将每次中奖奖金数额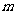 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com