2. 若对任意实数x、y总有f(xy)＝f(x)+f(y)，则下列各式中错误的是(　 )

(A)f(1)＝0　　　　　　　　　　 (B)f(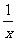)＝ f(x)　

(C)f(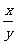)＝ f(x)－f(y)　　　 (D)f(xⁿ)＝nf(x)(n∈N)

1.已知：f(x+y)＝f(x)+f(y)对任意实数x、y都成立，则(　 )

(A)f(0)＝0　　　　　　　　　　 (B)f(0)＝1　

(C)f(0)＝0或1　　　　　　　　 (D)以上都不对

5.　　 三角函数型的抽象函数

f(x)＝tgx-------------------------- f(x+y)＝

f(x)＝cotx------------------------ f(x+y)＝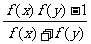

例1已知函数f(x)对任意实数x、y均有f(x+y)＝f(x)+f(y)，且当x>0时，f(x)>0，f(－1)＝ －2求f(x)在区间[－2,1]上的值域.

分析：先证明函数f(x)在R上是增函数(注意到f(x₂)＝f[(x₂－x₁)+x₁]＝f(x₂－x₁)+f(x₁))；再根据区间求其值域.

例2已知函数f(x)对任意实数x、y均有f(x+y)+2＝f(x)+f(y)，且当x>0时，f(x)>2，f(3)＝ 5，求不等式 f(a²－2a－2)<3的解.

分析：先证明函数f(x)在R上是增函数(仿例1)；再求出f(1)＝3；最后脱去函数符号.

例3已知函数f(x)对任意实数x、y都有f(xy)＝f(x)f(y)，且f(－1)＝1，f(27)＝9，当0≤x＜1时，f(x)∈[0，1].

(1)　　　 判断f(x)的奇偶性；

(2)　　　 判断f(x)在[0，+∞]上的单调性，并给出证明；

(3)　　　 若a≥0且f(a+1)≤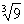，求a的取值范围.

分析：(1)令y＝－1；

　　 (2)利用f(x₁)＝f(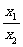·x₂)＝f(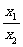)f(x₂)；

　　 (3)0≤a≤2.

例4设函数f(x)的定义域是(－∞，+∞)，满足条件：存在x₁≠x₂，使得f(x₁)≠f(x₂)；对任何x和y，f(x+y)＝f(x)f(y)成立.求：

(1)　　　 f(0)；

(2)　　　 对任意值x，判断f(x)值的符号.

分析：(1)令x= y＝0；(2)令y＝x≠0.

例5是否存在函数f(x)，使下列三个条件：①f(x)>0,x∈N；②f(a+b)＝ f(a)f(b)，a、b∈N；③f(2)＝4.同时成立？若存在，求出f(x)的解析式，若不存在，说明理由.

分析：先猜出f(x)＝2^x；再用数学归纳法证明.

例6设f(x)是定义在(0，+∞)上的单调增函数，满足f(x·y)＝f(x)+f(y)，f(3)＝1，求：

(1)　　　 f(1)；

(2)　　　 若f(x)+f(x－8)≤2，求x的取值范围.

分析：(1)利用3＝1×3；

(2)利用函数的单调性和已知关系式.

例7设函数y＝ f(x)的反函数是y＝g(x).如果f(ab)＝f(a)+f(b)，那么g(a+b)＝g(a)·g(b)是否正确，试说明理由.

分析：设f(a)＝m，f(b)＝n，则g(m)＝a，g(n)＝b，

进而m+n＝f(a)+f(b)＝ f(ab)＝f [g(m)g(n)]….

例8已知函数f(x)的定义域关于原点对称，且满足以下三个条件：

①　　 x₁、x₂是定义域中的数时，有f(x₁－x₂)＝；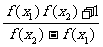

②　　 f(a)＝ －1(a＞0，a是定义域中的一个数)；

③　　 当0＜x＜2a时，f(x)＜0.

　　 试问：

(1)　　　 f(x)的奇偶性如何？说明理由；

(2)　　　 在(0，4a)上，f(x)的单调性如何？说明理由.

　　 分析：(1)利用f [－(x₁－x₂)]＝ －f [(x₁－x₂)]，判定f(x)是奇函数；

(3)　　　 先证明f(x)在(0，2a)上是增函数，再证明其在(2a，4a)上也是增函数.

　　 对于抽象函数的解答题，虽然不可用特殊模型代替求解，但可用特殊模型理解题意.有些抽象函数问题，对应的特殊模型不是我们熟悉的基本初等函数.因此，针对不同的函数要进行适当变通，去寻求特殊模型，从而更好地解决抽象函数问题.

　　 例9已知函数f(x)(x≠0)满足f(xy)＝f(x)+f(y)，

(1)　　　 求证：f(1)＝f(－1)＝0；

(2)　　　 求证：f(x)为偶函数；

(3)　　　 若f(x)在(0，+∞)上是增函数，解不等式f(x)+f(x－)≤0.

分析：函数模型为：f(x)＝log_a|x|(a＞0)

(1)　　　 先令x＝y＝1，再令x＝y＝ －1；

(2)　　　 令y＝ －1；

(3)　　　 由f(x)为偶函数，则f(x)＝f(|x|).

例10已知函数f(x)对一切实数x、y满足f(0)≠0，f(x+y)＝f(x)·f(y)，且当x＜0时，f(x)＞1，求证：

(1)　　　 当x＞0时，0＜f(x)＜1；

(2)　　　 f(x)在x∈R上是减函数.

分析：(1)先令x＝y＝0得f(0)＝1，再令y＝－x；

(3)　　　 受指数函数单调性的启发：

由f(x+y)＝f(x)f(y)可得f(x－y)＝，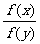

进而由x₁＜x₂，有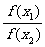＝f(x₁－x₂)＞1.

练习题：

4.　　 对数函数型的抽象函数

f(x)＝log_ax(a>0且a≠1)-----f(x·y)＝f(x)+f(y)；f(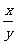)＝ f(x)－f(y)

3.　　 指数函数型的抽象函数

　 f(x)＝a^x------------------- f(x+y)＝f(x)f(y)；f(x－y)＝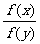

2.　　 幂函数型的抽象函数

　 f(x)＝x^a----------------f(xy)＝ f(x)f(y)；f()＝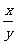

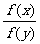
1.　　 正比例函数型的抽象函数

　　　 f(x)＝kx(k≠0)---------------f(x±y)＝f(x)±f(y)

3、　 求奇偶性，令y=-x；求单调性：令x+y=x₁

几类常见的抽象函数

2、　 令x=0或1来求出f(0)或f(1)

1、　 代y=x，