
4.“阳光想渗透所有的语言,春天把美好的故事传说。”“阳光”有着丰富的象征意义,下列说法不正确的是 A.从希腊奥林匹亚采集的奥运圣火的传递在全人类传播着和平、友谊、进步的共同心声
B.太阳祟拜是世界性的文化现象,如美国的登月工程就取名于美洲先民传说中的太阳神“阿波罗” C.阳光渗透到文化艺术的不同领域.如音乐作品《我的太阳》、绘画作品《日出·印象》等
D.人们常以“早晨的太阳”比喻人生的青春岁月、以“阳光”比喻健康的心态等
[解析]1969年7月,美国发射了载人航天器,成功地着落在月球上,人类第一次实现了踏上月球的理想。这个航天器是以古希腊的著名神话人物太阳神阿波罗命名的。
答案:B
3.下图描绘了美丽的乡村风景,画面构图完整。要完成此构图,你在写生时应选择的位置是
[解析]根据透视原理和图中的道路,可判断出,透视点选在B。
答案:B
[解析]太阳光经过三棱镜后可分为红、橙、黄、绿、蓝、靛、紫七色光,这种现象叫做光的色散. 因为同一种介质对各种单色光的折射率不同,所以通过三棱镜时,各单色光的偏折角不同。因此,白色光通过三棱镜会将各单色光分开,即色散。 凹面镜对光线有聚焦作用,所以可用来制作太阳灶等;凸面镜对光线有发散作用,汽车两恻的反光镜就是利用凸面镜制作的。
答案:D
2.某些画家根据光色原理对绘画色彩进行了大胆革新,打破了传统绘画的褐色调子,并直接面对自然风景写生,将光色瞬间变幻的效果记录下来。这一绘画流派是 A.古典主义 B.浪漫主义 C.印象主义 D.现代主义
[解析]18世纪末至19世纪初,法国大革命时期在资产阶级对古代希腊罗马英雄主义精神的追求中,新古典主义终于诞生了。这时的古典主义提倡典雅崇高的题材,庄重单纯的形式,强调理性而轻视情感,强调素描完整性和准确性、贬低色彩与笔触的表现,追求构图的均衡与完整,努力使作品产生一种古代的静穆而严峻的美,拿破仑统治结束后,人民对资产阶级启蒙思想推崇的“理性王国”感到失望,寻求新的精神的寄托,这种情绪反映在美术创作中,就产生了浪漫主义美术,它注重表现人的感情,运用鲜明色彩和奔放笔法,强调画面整体的完整和统一,但不拘泥于局部和细节的过分描绘和刻画,特别强调色彩的作用,使画面丰富多彩,辉煌瑰丽。19世纪中期,兴起了注重表现社会现实的现实主义美术,法国米勒的作品主要反映农民的生活和情感;俄罗斯画家列宾满怀强烈的民族忧患意识,深刻展现了俄国的社会现实,对劳动人民的悲惨处境寄于深切同情,表达了探明对美好生活的憧憬和渴望。19世纪后半期,随着社会经济的发展和科学技术的进步,一批青年画家以“不关心主题思想”为宗旨,反抗保守陈腐的主题思想,他们借助当时光学领域的新成就,醉心于光和色的研究,强调捕捉捉光和色之下世界万物的“瞬间印象”,表现微妙的色彩变化。题目中的描述符合印象主义的特点,故选C。
答案:C
21、在平面直角坐标系中,已知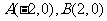 ,
, 为平面内一动点,直线
为平面内一动点,直线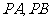 的斜率之积为
的斜率之积为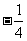 ,记动点
,记动点 的轨迹为
的轨迹为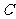 .
.
(1) 求曲线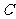 的轨迹方程;
的轨迹方程;
(2)若点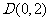 ,点
,点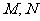 是曲线
是曲线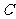 上的两个动点,且
上的两个动点,且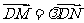 ,求实数
,求实数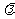 的取值范围.
的取值范围.
20、设抛物线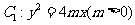 的准线与
的准线与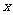 轴交于
轴交于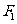 ,焦点为
,焦点为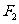 ,以
,以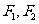 为焦点,离心率为
为焦点,离心率为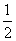 的椭圆
的椭圆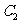 与抛物线
与抛物线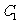 的一个交点为
的一个交点为 .
.
(1)若椭圆的长半轴长为2,求抛物线方程;
(2)在(1)的条件下,直线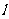 经过椭圆
经过椭圆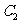 的右焦点
的右焦点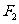 ,与抛物线
,与抛物线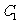 交于
交于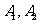 两点,如果
两点,如果
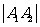 等于
等于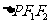 的周长,求
的周长,求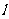 的斜率;
的斜率;
(3)是否存在实数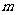 ,使得
,使得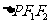 的边长是连续的自然数?若存在,求出
的边长是连续的自然数?若存在,求出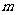 的值,若不存
的值,若不存
在,说明理由.
19、已知顶点在原点,焦点在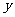 轴上的抛物线过点
轴上的抛物线过点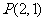 .
.
(1)求抛物线的标准方程;
(2)过点 作直线
作直线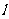 与抛物线有且只有一个公共点,求直线
与抛物线有且只有一个公共点,求直线 的方程;
的方程;
(3)过点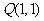 作直线交抛物线于
作直线交抛物线于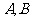 两点,使得
两点,使得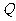 恰好平分线段
恰好平分线段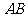 ,求直线
,求直线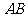 的方程.
的方程.
18、一个口袋中装有1个红球和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(1)求一次摸奖就中奖的概率;
(2)设三次摸奖(每次摸奖后放回)中奖的次数为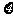 ,求
,求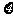 的分布列及期望值.
的分布列及期望值.
17、已知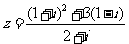
(1)求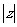 ; (2)若
; (2)若 ,求实数
,求实数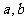 的值.
的值.
14._____ __ 15. 16.
11. 12. 13.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com