
3. 求复杂的事件的概率时,通常有两种方法:一是将所求事件的概率化为一些彼此互斥的事件的概率的和,二是先去求此事件的对立事件的概率。
2. 要熟练地应用概念来处理解决问题。
1. 求等可能事件的概率,首先要确定试验的所有基本事件数及所求事件中包含的基本事件数。
例1、抛掷两枚均匀的正八面体的骰子(它们的每个面上分别标有数字1,2,3,4,5,6,7,8)。试求:(1)出现“点数和为5”的概率;(2)出现“点数和为几”的概率最大,并求出此时的概率。
例2、蚂蚁A位于数轴x=0处,蚂蚁B位于x=2处,
这两只蚂蚁每隔一秒钟向左或向右移动一个单位,设它们向右移动的概率为 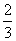 ,向左移动的概率为
,向左移动的概率为 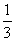 。
。
(1)求3秒后,蚂蚁A在x=1处的概率;(2)求4秒后,蚂蚁A、B同时在x=2处的概率。
例3、(2005湖北) 某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为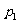 ,寿命为2年以上的概率为
,寿命为2年以上的概率为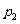 .从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
.从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
(Ⅰ)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率;
(Ⅱ)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;
(Ⅲ)当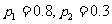 时,求在第二次灯泡更换工作,至少需要更换4只灯泡的概率(结果保留两个有效数字).
时,求在第二次灯泡更换工作,至少需要更换4只灯泡的概率(结果保留两个有效数字).
备用题:右表为某班英语、数学的成绩分布,全班共有学生50人,成绩分为1~5五个档次。例如表中英语成绩为4分、数学成绩为2分的学生共5人,设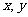 分别表示英语成绩和数学成绩。
分别表示英语成绩和数学成绩。
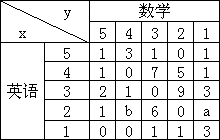 (1)
(1)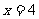 的概率为多少?
的概率为多少?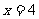 且
且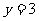 的概率为多少?
的概率为多少?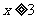 的概率为多少?在
的概率为多少?在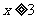 的基础上,
的基础上,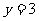 同时成立的概率为多少?
同时成立的概率为多少?
(2)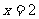 的概率为多少?
的概率为多少? 的值是多少?
的值是多少?
(3)如果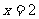 及
及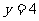 相互独立,
相互独立,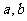 的值分别
的值分别
为多少?
4.(2004南通)五副不同的手套进行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只。 (1)求下列事件的概率:①A:甲正好取得两只配对手套;②B:乙正好取得两只配对手套;(2)A和B是否独立?并证明你的结论。
3.甲、乙两人独立地解同一问题,甲解决这个问题的概率是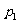 ,乙解决这个问题的概率是
,乙解决这个问题的概率是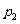 ,那么恰好有1人解决这个问题的概率是 ( )
,那么恰好有1人解决这个问题的概率是 ( )
A.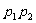 B.
B.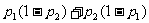
C.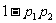 D.
D.
2.在圆周上有10个等分点,以这些点为顶点,每3个点可以构成一个三角形,如果随机选择3个点,刚好构成直角三角形的概率是( )
A. 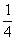 B.
B.
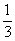 C.
C.
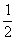 D.
D.
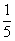
1.某轻轨列车有4节车厢,现有6位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为 .
4、加强对概率的三种形式的理解和应用,能熟练应用这些知识解决一些实际应用问题。
3、会计算事件在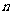 次独立重复试验中发生
次独立重复试验中发生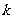 次的概率;
次的概率;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com