
9.解:(Ⅰ)记甲、乙、丙三台机器在一小时需要照顾分别为事件A、B、C,
则A、B、C相互独立,
由题意得: P(AB)=P(A)·P(B)=0.05
P(AC)=P(A)·P(C)=0.1
P(BC)=P(B)·P(C)=0.125
解得:P(A)=0.2;P(B)=0.25;P(C)=0.5
所以, 甲、乙、丙每台机器在这个小时内需要照顾的概率分别是0.2、0.25、0.5
(Ⅱ)∵A、B、C相互独立,∴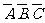 相互独立,
相互独立,
∴甲、乙、丙每台机器在这个小时内需都不需要照顾的概率为
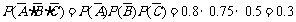
∴这个小时内至少有一台需要照顾的概率为
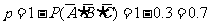
1. 途经10个停靠点,没有一个停靠点出发后,乘客人数超过18人的概率为
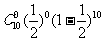
途经 10个停靠点,只有一个停靠点出发后,乘客人数超过18人的概率
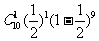
所以,途经10个停靠点,有2个以上(含2个)停靠点出发后,乘客人数超过18人的概率
P=1-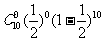 -C
-C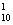 (
(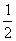 )(1-
)(1-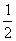 )9=1-
)9=1-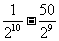 =
=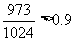
∴该线路需要增加班次。
答:(Ⅰ)每个停靠点出发后,乘客人数不超过24人的概率约为0.7
(Ⅱ) 该线路需要增加班次
0. (Ⅱ)从每个停靠点出发后,乘客人数超过18人的概率为0.20+0.20+0.1=0.5
0.1+0.15+0.25+0.2=0.7
8.解:(Ⅰ)每个停靠点出发后,乘客人数不超过24人的概率约为
7.(1)甲获得3枚商标的概率为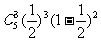 ;甲获得4枚商标的概率为
;甲获得4枚商标的概率为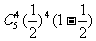 ;甲获得5枚商标的概率为
;甲获得5枚商标的概率为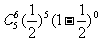 ;所以甲至少获得3枚商标的概率为
;所以甲至少获得3枚商标的概率为
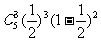 +
+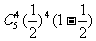 +
+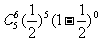 =
=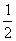
(2)甲、乙两选手至少有一位获得1个或1个以上的商标的概率为
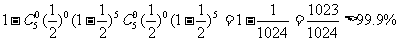 ,故有把握断定。
,故有把握断定。
1.A 2.(1)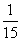 (2)
(2)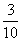 3.200 4.C 5.D 6.
3.200 4.C 5.D 6.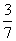
4.(1)P(A)=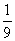 , P(B)=
, P(B)= 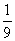 , (2)
P(AB)=
, (2)
P(AB)=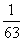 ,P(A)P(B)=
,P(A)P(B)=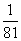 ,所以A、B不独立。
,所以A、B不独立。
[例题探究]
例1.(1)在一次抛骰子的过程中,每个点数出现的概率都是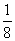 ,点数和为5共有四种情况,故所求概率为
,点数和为5共有四种情况,故所求概率为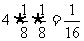
(2)点数和为9的概率最大,共有八种情况,故概率为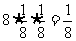
[教学建议]从等可能概率事件的基本事件出发,引导学生寻找答案。
例2.(1)蚂蚁A在三次移动中,恰有两次向右移动,故其发生的概率为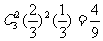
(2)蚂蚁A在四次移动中,恰有三次向右移动,一次向左移动,且同时蚂蚁B在四次移动中恰有两次向右移动,两次向左移动。故其发生的概率为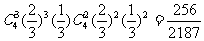
[教学建议]本题关键是转化问题,即将本题转化为一个独立重复事件的概率来求。在教学中,要引导学生合理地进行转化。
例3.解:(I)在第一次更换灯泡工作中,不需要换灯泡的概率为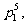 需要更换2只灯泡的概率为
需要更换2只灯泡的概率为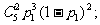
(II)对该盏灯来说,在第1、2次都更换了灯泡的概率为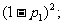 在第一次未更换灯泡而在第二次需要更换灯泡的概率为
在第一次未更换灯泡而在第二次需要更换灯泡的概率为 故所求的概率为
故所求的概率为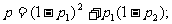
(III)至少换4只灯泡包括换5只和换4只两种情况,换5只的概率为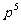 (其中
(其中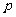 为(II)中所求,下同)换4只的概率为
为(II)中所求,下同)换4只的概率为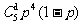 ,故至少换4只灯泡的概率为
,故至少换4只灯泡的概率为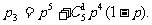
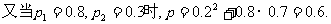
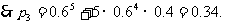
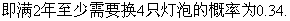
备用题:(1)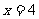 的概率为
的概率为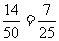 ;
;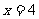 且
且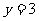 的概率为
的概率为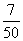 ;
;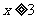 的概率为
的概率为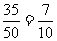 ;在
;在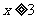 的基础上,
的基础上,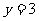 同时成立的概率为
同时成立的概率为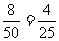 。
。
(2)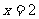 的概率为
的概率为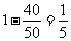 ;
; 的值是3。
的值是3。
(3)如果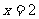 及
及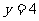 相互独立,
相互独立,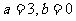 。
。
冲刺强化训练(26)
1. 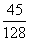 2.B 3.B
2.B 3.B
9、(2005全国)设甲、乙、丙三台机器是否需要照顾相互之间没有影响。已知在某一小时内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125,
(Ⅰ)求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少;
(Ⅱ)计算这个小时内至少有一台机器需要照顾的概率.
第26讲 概率
[课前热身]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com