
6.如图6所示,通电直导线cd右侧有一个金属框与导线cd在同一平面内,金属棒ab放在框架上,若ab受到向左的磁场力,则cd中电流的变化情况是( )
A.cd中通有由d→c方向逐渐减小的电流
B.cd中通有由d→c方向逐渐增大的电流
 C.cd中通有由c→d方向逐渐减小的电流
C.cd中通有由c→d方向逐渐减小的电流
D.cd中通有由c→d方向逐渐增大的电流
4.已知神舟七号飞船在离地球表面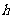 高处的轨道上做周期为
高处的轨道上做周期为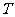 的匀速圆周运动,地球的半径
的匀速圆周运动,地球的半径 ,万有引力常量为
,万有引力常量为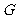 。在该轨道上,神舟七号航天飞船 ( )
。在该轨道上,神舟七号航天飞船 ( )
A.运行的线速度大小为
B.运行的线速度小于第一宇宙速度
C.运行时的向心加速度大小
D.地球表面的重力加速度大小为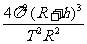
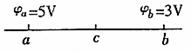 5.如图所示,a、c、b为同一条电场线上的三点,c为ab中点。a、b电势分别为
5.如图所示,a、c、b为同一条电场线上的三点,c为ab中点。a、b电势分别为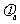 =5V,
=5V, 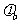 =3V,则 ( )
=3V,则 ( )
A.c点的电势一定为4V
B.a点的场强一定比b点场强大
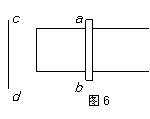 C.a点的场强与b点的场强一定相等
C.a点的场强与b点的场强一定相等
D.正电荷从c点运动到b点电势能一定减少
3.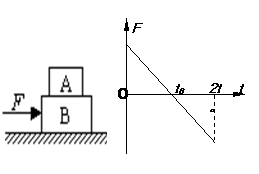 A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图所示,A、B始终相对静止,则在
A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图所示,A、B始终相对静止,则在 时间内,下列说法不正确的是( )
时间内,下列说法不正确的是( )
A.t0时刻,A、B间静摩擦力最大
B.t0时刻,A、B速度最大
C.2t0时刻,A、B速度最小
D.2t0时刻,A、B位移最大
2.某科技创新小组设计制作出一种全自动升降机模型,用电动机通过钢丝绳拉着升降机由静止开始匀加速上升,已知升降机的质量为m,当升降机的速度为v1时,电动机的有用功率达到最大值P,以后电动机保持该功率不变,直到升降机以最大速度v2匀速上升为止,整个过程中忽略摩擦阻力及空气阻力,重力加速度为g。有关此过程下列说法正确的是:( )
A.钢丝绳的最大拉力为
B.升降机的最大速度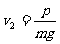
C.钢丝绳的拉力对升降机所做的功等于升降机克服重力所做的功
D.升降机速度由v1增大至v2的过程中,钢丝绳的拉力不断减小
1.汽车A在红绿灯前停住,绿灯亮起时起动,以0.4m/s2的加速度做匀加速运动,经过30s后以该时刻的速度做匀速直线运动,设在绿灯亮的同时,汽车B以8m/s的速度从A车旁驶过且一直以此速度做匀速直线运动,速度方向与A车相同,则从绿灯开始亮时开始:( )
A、A车在加速过程中与B车相遇 B、A、B相遇时,速度相同
C、相遇时A车做匀速运动 D、两车相遇后不可能再次相遇
(17)(本小题满分12分)
设平面上向量 ,
, ,
, 与
与 不共线,
不共线,
(Ⅰ)证明向量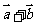 与
与 垂直;
垂直;
(Ⅱ)若两个向量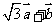 与
与 的模相等,试求角
的模相等,试求角 .
.
(18)(本小题满分12分)
袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.
(Ⅰ)若有放回地摸出4个球,求取出的红球数不小于黑球数的概率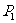 ;
;
(Ⅱ)若无放回地摸出4个球,
①求取出的红球数ξ的概率分布列和数学期望;
②求取出的红球数不小于黑球数的概率 ,并比较
,并比较 的大小.
的大小.
 (19) (本小题满分12分)
(19) (本小题满分12分)
如图,已知正三棱柱 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱 的中点,平面ABD和平面
的中点,平面ABD和平面 的交线为MN.
的交线为MN.
(Ⅰ)试证明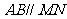 ;
;
(Ⅱ)若直线AD与侧面 所成的角为
所成的角为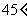 ,试求二面角
,试求二面角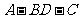 的大小.
的大小.
(20)(本小题满分12分)
已知椭圆 的离心率
的离心率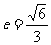 ,
, 为过点
为过点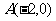 和上顶点
和上顶点 的直线,下顶点
的直线,下顶点 与
与 的距离为
的距离为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的动弦 交
交 于
于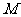 , 若
, 若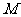 为线段
为线段 的中点,线段
的中点,线段 的中垂线和x轴交点为
的中垂线和x轴交点为 ,试求
,试求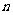 的范围.
的范围.
(21)(本小题满分12分)
已知 ,
, ,对任意实数
,对任意实数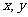 满足:
满足: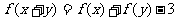
(Ⅰ)当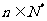 时求
时求 的表达式
的表达式
(Ⅱ)若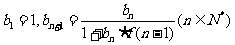 ,求
,求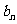
(III)记 ,试证
,试证 .
.
(22)(本小题满分14分)
已知定义在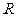 上的奇函数
上的奇函数 在
在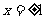 处取得极值.
处取得极值.
(Ⅰ)求函数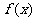 的解析式;
的解析式;
(Ⅱ)试证:对于区间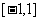 上任意两个自变量的值
上任意两个自变量的值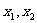 ,都有
,都有 成立;
成立;
(Ⅲ)若过点 可作曲线
可作曲线 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.
(13)已知 ,则
,则 .
.
(14)设函数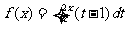 ,则
,则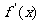 =__________.
=__________.
(15)平面上存在点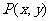 满足
满足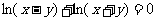 ,那么
,那么 的最小值是 .
的最小值是 .
(16)在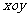 坐标平面内,若关于
坐标平面内,若关于 的不等式
的不等式 表示三角形区域,则实参数
表示三角形区域,则实参数 的取值集合为________.
的取值集合为________.
(1) 定义集合运算: 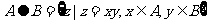 .设
.设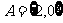 ,
, ,则集合
,则集合 的所有元素之和为( )
的所有元素之和为( )
A.6 B.8 C. 12 D.16
(2) 某单位有老年人28人,中年人56人,青年人80人,为了调查他们的身体情况,需从他们中抽取一个容量为41的样本,则适合的抽取方法是( )
A.简单随机抽样法 B.抽签法 C.随机数表法 D.分层抽样法
(3) 已知直线a和平面 内的射影分别是b、c,则b、c的位置关系是(
)
内的射影分别是b、c,则b、c的位置关系是(
)
①相交 ②平行 ③异面
A. ①② B. ①②③ C. ②③ D. ①③
(4) 过抛物线 的焦点作直线与其交于M、N两点,作平行四边形
的焦点作直线与其交于M、N两点,作平行四边形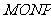 ,则P点的轨迹方程为( )
,则P点的轨迹方程为( )
A.  B.
B. 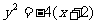 C.
C. 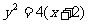 D.
D. 
(5)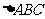 的三边
的三边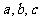 满足等式
满足等式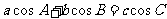 ,则此三角形必是( )
,则此三角形必是( )
A、以 为斜边的直角三角形
B、以
为斜边的直角三角形
B、以 为斜边的直角三角形
为斜边的直角三角形
C、等边三角形 D、其它三角形
(6) 记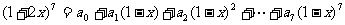 ,则
,则 的值为( )
的值为( )
A.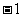 B.
B.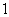 C.
C. D.
D.
(7)函数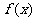 是定义域为R的奇函数,且
是定义域为R的奇函数,且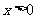 时,
时,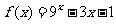 ,则函数
,则函数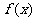 的零点个数是( )
的零点个数是( )
A.1 B.2 C.3 D.4
(8)6名志愿者随机进入2个不同的全运场馆参加接待工作,则每个场馆至少有两名志愿者的概率为( )
 A.
A.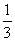 B.
B.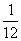 C.
C. D.
D.
(9)给出右面的程序框图,那么,输出的数是( )
A.3 B. 5 C.7 D.9
(10)定义“等比数列” :
:
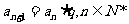 ,则在复平面内
,则在复平面内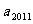 所对应的点在( )
所对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(11)已知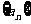 是递减等比数列,
是递减等比数列, ,则
,则 的取值范围是(
)
的取值范围是(
)
A.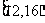 B.
B. C.
C.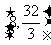 D.
D.
(12)已知函数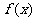 的定义域为
的定义域为 ,导函数为
,导函数为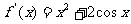 且
且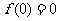 ,则满足
,则满足 的实数
的实数 的取值范围为( )
的取值范围为( )
A. B.
B. ) C.
) C. D.
D. )
)
第II卷(非选择题 90 分)
22.(本小题满分14分)
已知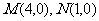 ,若动点
,若动点 满足
满足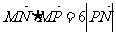 .
.
(1)求动点 的轨迹
的轨迹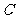 的方程;
的方程;
(2)设过点 的直线
的直线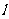 交轨迹
交轨迹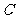 于
于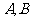 两点,若
两点,若 ,求直线
,求直线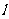 的斜
的斜
率的取值范围。
21.(本小题满分12分)
已知函数 (
( ).
).
(1)若函数 处取得极值,且极小值为
处取得极值,且极小值为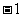 ,求
,求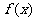 的解析式;
的解析式;
(2)若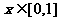 ,函数
,函数 图象上的任意一点的切线斜率为
图象上的任意一点的切线斜率为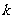 ,求
,求 恒成立时a
恒成立时a
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com