
19.本题主要考查将实际问题转化为数学问题的能力,以及综合运用函数知识解决问题的能力.满分13分.
解 设供应站坐标为 ,各工作台上的所有工人到供应站的距离之和为
,各工作台上的所有工人到供应站的距离之和为 .
.
(Ⅰ)由题设知,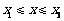 ,所以
,所以
 ……
…… 分
分
 . ……
. …… 分
分
故当 时,
时, 取最小值,此时供应站的位置为
取最小值,此时供应站的位置为 . ……
. ……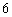 分
分
(Ⅱ)由题设知,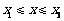 ,所以各工作台上的所有工人到供应站的距离之和为
,所以各工作台上的所有工人到供应站的距离之和为
 . ……
. …… 分
分
且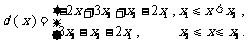 ……
…… 分
分
因此,函数 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上是常数.故供应站位置位于区间
上是常数.故供应站位置位于区间 上任意一点时,均能使函数
上任意一点时,均能使函数 取得最小值,且最小值为
取得最小值,且最小值为 ,
, . ……
. …… 分
分
18. 本题主要考查线线,线面关系的基础知识,同时考查空间想象能力和推理运算能力.满分12分.
本题主要考查线线,线面关系的基础知识,同时考查空间想象能力和推理运算能力.满分12分.
解 (Ⅰ)因为 ,
, 分别是
分别是 ,
, 的中点,
的中点,
所以 ,因此
,因此 是异面直线
是异面直线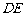
与 所成的角. ……
所成的角. …… 分
分
又因为 是圆
是圆 的的直径,点
的的直径,点 是弧
是弧 的
的
中点,所以 是以
是以 为直角的等腰
为直角的等腰
直角三角形.于是 .
.
故异面直线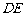 与
与 所成的角为
所成的角为 .
.
……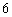 分
分
(Ⅱ)因为 平面
平面 ,
,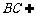 平面
平面 ,所以
,所以 . ……
. …… 分
分
由(Ⅰ)知, ,所以
,所以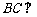 平面
平面 .
……
.
…… 分
分
又由(Ⅰ)知, ,故
,故 平面
平面 .
……
.
…… 分
分
17.本题主要考查平均数、方差、抽样、概率等基础知识以及分析问题和解决问题的能力.满分12分.
解 (Ⅰ)甲射击命中的环数的平均数为 ,
,
其方差为 . ……
. …… 分
分
乙射击命中的环数的平均数为 ,
,
其方差为 . ……
. …… 分
分
因此 ,
, ,故甲,乙两人射击命中的环数的平均数相同,但甲比乙发挥较稳定. ……
,故甲,乙两人射击命中的环数的平均数相同,但甲比乙发挥较稳定. ……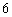 分
分
(Ⅱ)由(Ⅰ)知,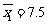 .
.
设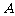 表示事件“样本平均数与总体平均数之差的绝对值不超过
表示事件“样本平均数与总体平均数之差的绝对值不超过 ”.
”.
从总体中抽取两个个体的全部可能的结果 ,
,


 ,
, ,
, ,共15个结果.其中事件
,共15个结果.其中事件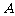 包含的结果有
包含的结果有

 ,
,


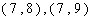 ,共有
,共有 个结果. ……
个结果. …… 分
分
故所求的概率为 . ……
. …… 分
分
16.本题主要考查向量、三角函数的基础知识,同时考查根据相关公式合理变形、正 确运算的能力.满分12分.
解 (Ⅰ) 由 ,得
,得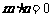 ,即
,即 . ……
. …… 分
分
所以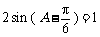 ,即
,即 .
.
因为 ,所以
,所以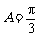 . ……
. ……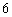 分
分
(Ⅱ)由 ,得
,得 . ……
. …… 分
分
依正弦定理,得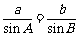 ,即
,即 . ……
. …… 分
分
解得, . ……
. …… 分
分
15.(1) ; (2)
; (2)
说明:第15题中的第一空3分,第二空2分.
13. 14.
14.
9. 10.
10. 11.
11. 12.
12.
5.B 6.C 7.B 8.
1.B 2. 3.D 4.C
3.D 4.C
21.(本小题满分13分)
如图6所示,在直角坐标平面上的矩形 中,
中, ,
, ,点
,点 ,
, 满足
满足 ,
, ,点
,点 是
是 关于原点的对称点,直线
关于原点的对称点,直线 与
与 相交于点
相交于点 .
.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
 (Ⅱ)若过点
(Ⅱ)若过点 的直线与点
的直线与点 的轨迹相交于
的轨迹相交于 ,
,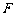 两点,求
两点,求 的面积的最大值.
的面积的最大值.
|
2010湖南省高考适应性测试
数学(文科)试题 参考解答及评分标准
说明:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com