
7.求函数解析式的常用方法:
(1)待定系数法―已知 为二次函数,且
为二次函数,且 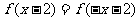 ,且f(0)=1,图象在x轴上截得的线段长为2
,且f(0)=1,图象在x轴上截得的线段长为2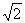 ,求
,求 的解析式 。(答:
的解析式 。(答: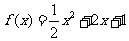 )
)
(2)配凑法―(1)已知 求
求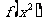 的解析式___(答:
的解析式___(答: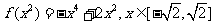 );(2)若
);(2)若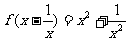 ,则函数
,则函数 =___(答:
=___(答: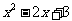 );
);
(3)方程的思想―已知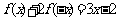 ,求
,求 的解析式(答:
的解析式(答: );
);
6.分段函数的概念。(1)设函数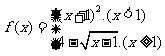 ,则使得
,则使得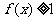 的自变量
的自变量 的取值范围是____(答:
的取值范围是____(答: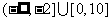 );(2)已知
);(2)已知 ,则不等式
,则不等式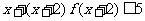 的解集是___(答:
的解集是___(答: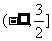 )
)
5.求函数值域(最值)的方法:
(1)配方法―(1)当 时,函数
时,函数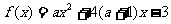 在
在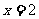 时取得最大值,则
时取得最大值,则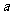 的取值范围是___(答:
的取值范围是___(答: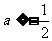 );
);
(2)换元法(1)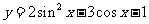 的值域为_____(答:
的值域为_____(答: );(2)
);(2)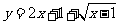 的值域为_____(答:
的值域为_____(答: )(令
)(令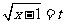 ,
,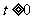 。运用换元法时,要特别要注意新元
。运用换元法时,要特别要注意新元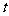 的范围);3)
的范围);3) 的值域为____(答:
的值域为____(答: );(4)
);(4)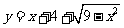 的值域为____(答:
的值域为____(答: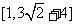 );
);
(3)函数有界性法―求函数 ,
, ,
, 的值域(答:
的值域(答: 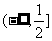 、(0,1)、
、(0,1)、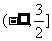 );
);
(4)单调性法――(江西卷3)若函数 的值域是
的值域是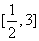 ,则函数
,则函数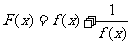 的值域是B
的值域是B
A.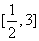 B.
B. C.
C.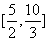 D.
D.
(5)数形结合法――已知点 在圆
在圆 上,求
上,求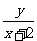 及
及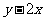 的取值范围(答:
的取值范围(答: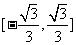 、
、 );
);
(6)不等式法―设 成等差数列,
成等差数列,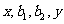 成等比数列,则
成等比数列,则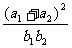 的取值范围是____________.(答:
的取值范围是____________.(答: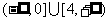 )。
)。
(7)导数法―求函数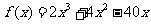 ,
,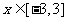 的最小值。(答:-48)
的最小值。(答:-48)
4.研究函数问题时要树立定义域优先的原则):
(1)(2009江西卷理)函数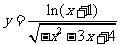 的定义域为
的定义域为
A.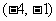 B.
B. C.
C. D.
D.
答案:C
[解析]由 .故选C
.故选C
(2)设函数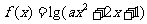 ,①若
,①若 的定义域是R,求实数
的定义域是R,求实数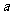 的取值范围;②若
的取值范围;②若 的值域是R,求实数
的值域是R,求实数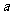 的取值范围(答:①
的取值范围(答:① ;②
;②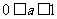 )
)
(2)复合函数的定义域:
(1)若函数 的定义域为
的定义域为 ,则
,则 的定义域为__________(答:
的定义域为__________(答: );
);
(2)若函数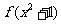 的定义域为
的定义域为 ,则函数
,则函数 的定义域为________(答:[1,5]).
的定义域为________(答:[1,5]).
3.若解析式相同,值域相同,但其定义域不同的函数,则称这些函数为“天一函数”,那么解析式为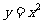 ,值域为{4,1}的“天一函数”共有__个(答:9)
,值域为{4,1}的“天一函数”共有__个(答:9)
2.函数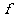 : A
: A B是特殊的映射。设集合
B是特殊的映射。设集合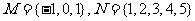 ,映射
,映射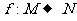 满足条件“对任意的
满足条件“对任意的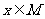 ,
, 是奇数”,这样的映射
是奇数”,这样的映射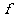 有____个(答:12)
有____个(答:12)
(
12.一元二次方程根的分布理论。
(1)实系数方程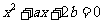 的一根大于0且小于1,另一根大于1且小于2,则
的一根大于0且小于1,另一根大于1且小于2,则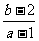 的取值范围是_________(答:(
的取值范围是_________(答:( ,1))
,1))
(2)不等式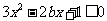 对
对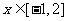 恒成立,则实数
恒成立,则实数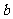 的取值范围是____(答:
的取值范围是____(答: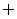 )。
)。
11. 对于方程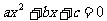 有实数解的问题。
有实数解的问题。
(1)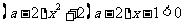 对一切
对一切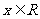 恒成立,则
恒成立,则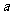 的取值范围是_______(答:
的取值范围是_______(答: );
);
(2)若在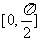 内有两个不等的实根满足等式
内有两个不等的实根满足等式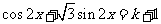 ,则实数
,则实数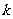 的范围是_______.(答:
的范围是_______.(答: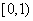 )
)
10. 一元二次不等式的解集:
(2009福建卷理)已知全集U=R,集合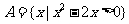 ,则
,则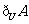 等于
等于
A. { x ∣0 x
x 2}
B { x ∣0<x<2}
2}
B { x ∣0<x<2}
C. { x ∣x<0或x>2}
D { x ∣x 0或x
0或x 2}
2}
[答案]:A
[解析]∵计算可得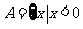 或
或 ∴
∴ .故选A
.故选A
(2009安徽卷理)若集合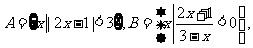 则A∩B是
则A∩B是
(A) 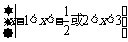 (B)
(B) 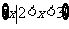 (C)
(C)
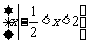 (D)
(D) 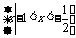
[解析]集合 ,∴
,∴ 选D
选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com