23、(本题10分)如图，从一个半径为1的圆形铁皮中剪下一个圆心角为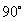的扇形BAC．

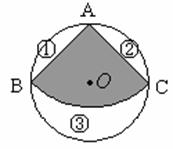(1)求这个扇形的面积；

(2)若将扇形BAC围成一个圆锥的侧面，这个圆锥的底面直径是多少？

能否从最大的余料③中剪出一个圆做该圆锥的底面？请说明理由．

22、(10分)某体育用品商场为推销某一品牌运动服，先做了市场调查，得到数据如下表：

(1)以x作为点的横坐标，p作为纵坐标，把上表中的数据，在图中的直角坐标系中描出相应的点，观察连结各点所得的图形，判断p与x的函数关系，并求出p与x的函数关系式；

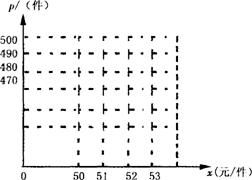
(2)如果这种运动服的买入价为每件40元，试求销售利润y(元)与卖出价格x(元／件)的函数关系式(销售利润=销售收入-买入支出)；

(3)在(2)的条件下，当卖出价格为多少时，能获得最大利润?

21、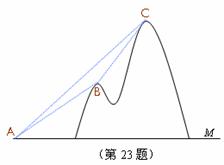(本题8分)如图，某电信公司计划修建一条连接B、C两地的电缆。测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B处测得C地的仰角为60°，已知C地比A地高200m，求电缆BC的长(结果保留根号).

20、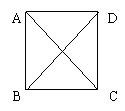(本题8分)在平面上有且只有四个点，这四个点有一个独特的性质：每两点之间的距离有且只有两种长度，例如正方形ABCD四个顶点A，B，C，D，有AB=BC=CD=DA,AC=BD，请画出具有这种独特性质的另外四种不同的图形，并标明相等的线段 　

19、(本题6分)桌面上有15张扑克牌，甲、乙两人轮流取，每次最少取一张，最多取三张，谁取走最后一张谁就赢。

(1)这个游戏规则对于甲、乙两方公平吗？

(2)是先取者毕胜，还是后取者毕胜？有何致胜秘诀？

(3)若将上面的15张扑克换成n张(n是不小于4的正整数)，情况有如何？　

18、(本小题6分)以O点为位似中心，在按位似比为2：1将图形缩小，请在O的另一侧画出它的位似图形。

17．(本题6分)求下列各式的值：

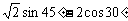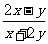(1)+　　　　 (2)已知，求的值.　

16、如右图，直角三角形ABC中，∠C=90°，∠A=30°，点0在斜边AB上，半径为2的⊙O过点B，切AC边于点D，交BC边于点E，则由线段CD，CE及弧DE围成的隐影部分的面积为　　　　　　

15、从1到10这十个自然数中，任意取出两个数，它们的积大于10的概率是　　　。

14、已知关于x的一元二次方程m²x²+(2m-1)x+1=0有两个不相等的实数根，则m的取值范围是