
2.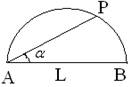 如图所示,电量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L.在以L为直径的光滑绝缘的半圆环上,穿有负点电荷q(不计重力)且在P点平衡,PA与AB夹角为α,则
如图所示,电量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L.在以L为直径的光滑绝缘的半圆环上,穿有负点电荷q(不计重力)且在P点平衡,PA与AB夹角为α,则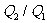 应为( )
应为( )
A.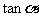 B.
B.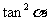 C.
C.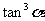 D.
D.
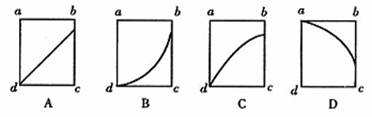
1. 如图所示,光滑水平桌面上,一小球以速度v向右匀速运动,当它经过靠近桌边的竖直木板的ad边正前方时,木板开始作自由落体运动.若木板开始运动时,cd边与桌面相齐,则小球在木板上的正投影轨迹是(
)
如图所示,光滑水平桌面上,一小球以速度v向右匀速运动,当它经过靠近桌边的竖直木板的ad边正前方时,木板开始作自由落体运动.若木板开始运动时,cd边与桌面相齐,则小球在木板上的正投影轨迹是(
)
9、证明:设点Pn的坐标是 ,由已知条件得
,由已知条件得
点Qn、Pn+1的坐标分别是:

由Pn+1在直线l1上,得 
所以
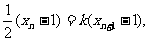 即
即 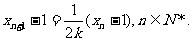
(Ⅱ)解:由题设知
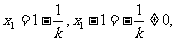 又由(Ⅰ)知
又由(Ⅰ)知  ,
,
所以数列 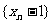 是首项为
是首项为 公比为
公比为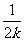 的等比数列.
的等比数列.
从而 
(Ⅲ)解:由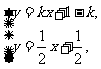 得点P的坐标为(1,1).
得点P的坐标为(1,1).
由(Ⅱ)知 其中
其中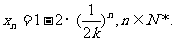
则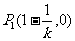
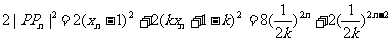
而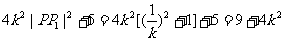
 ,
,
而此时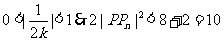 ,故
,故 ;
;
 ,
,
而此时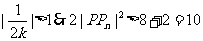 ,故
,故 ;
;
 ,
,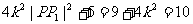
而此时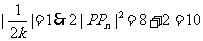 ,故
,故 。
。
8、21600
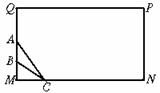
7、解:要使体温计AB观察的最清晰,只要视角∠ACB最大即可,以NN,NQ所在直线为x轴,y轴,以N为坐标原点建立直角坐标系.设C(x,0),∠ACB=θ, 3分
则tanθ=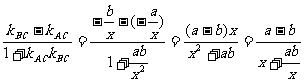
∵a>b,∴tanθ≤
等号当且仅当x=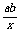 ,即x=
,即x=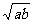 时成立.
时成立.
又θ∈(0, ),所以当x=
),所以当x=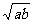 时,θ取最大值arctan
时,θ取最大值arctan .
.
故C点应在NN上距N为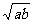 处.
处.
1、A 2、C
3、251,3;
4、61 5、B
6、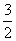 ,
,
1、6018 2、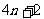 3、
3、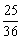 4、
4、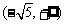
[例题探究]
例1、解:(1) 由题设得, ,从而
,从而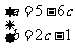 ,
,
所以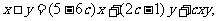 ∴
∴
∴ 对任意实数x都成立。
对任意实数x都成立。
∴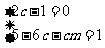 ,∴
,∴ 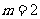 、
、
(2)
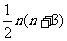
例2、解:(1)若要产生一常数数列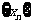 ,只需
,只需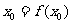 ,即:
,即: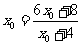
解得
(2) 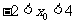
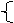 例3..解:(1)
例3..解:(1) 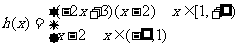
(2) 当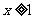 时, h(x)= (-2x+3)(x-2)=-2x2+7x-6=-2(x-
时, h(x)= (-2x+3)(x-2)=-2x2+7x-6=-2(x-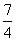 )2+
)2+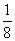 ,∴h(x)≤
,∴h(x)≤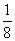 ;
;
当 时,
时, 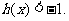 ∴当x=
∴当x=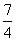 时, h(x)取得最大值是
时, h(x)取得最大值是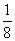
(3)解法一:令 f(x)=sinx+cosx, α=
则g(x)=f(x+α)= sin(x+ )+cos(x+
)+cos(x+ )=cosx-sinx,
)=cosx-sinx,
于是h(x)= f(x)·f(x+α)= (sinx+cosx)( cosx-sinx)=cos2x.
解法二:令f(x)=1+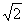 sinx, α=π,
sinx, α=π,
g(x)=f(x+α)=
1+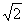 sin(x+π)=1-
sin(x+π)=1-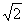 sinx,
sinx,
于是h(x)= f(x)·f(x+α)= (1+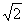 sinx)( 1-
sinx)( 1-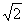 sinx)=cos2x.
sinx)=cos2x.
冲刺强化训练(28)
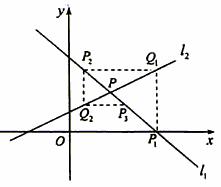
9、如图,直线 相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列
相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列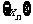 (Ⅰ)证明
(Ⅰ)证明
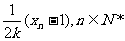 ;(Ⅱ)求数列
;(Ⅱ)求数列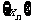 的通项公式;(Ⅲ)比较
的通项公式;(Ⅲ)比较 的大小.
的大小.
第28讲 新情景试题例举
[课前热身]
8、用n个不同的实数a1,a2,┄an可得n!个不同的排列,每个排列为一行写成 1 2 3
一个n!行的数阵.对第i行ai1,ai2,┄ain,记bi=- ai1+2ai2-3 ai3+┄+(-1)nnain, 1 3 2
i=1,2,3, ┄,n!.用1,2,3可你数阵如右,由于此数阵中每一列各数之和都 2 1 3
是12,所以,b1+b2+┄+b6=-12+2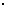 12-3
12-3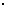 12=-24.那么,在用1,2,3,4,5形成 2 3 1
12=-24.那么,在用1,2,3,4,5形成 2 3 1
的数阵中,求 b1+b2+┄+b120的值. 3 1 2
3 2 1
7、如图所示,某化工厂反应塔MQ上有温度计AB.已知|AM|=a,|BM|=b.在矩形QMNP的边MN上建观察点C较安全,观察温度计AB时视角越大越清晰.问C在线段MN上何处时,对温度计AB观察得最清晰?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com