
16.(湖南师大附中2010届高三第五次月考试卷)为抗击金融风暴,某工贸系统决定对所属企业给予低息贷款的扶持.该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级分配相应的低息贷款金额,其评估标准和贷款金额如下表:
 为了更好地掌控贷款总额,该系统随机抽查了所属部分企业
为了更好地掌控贷款总额,该系统随机抽查了所属部分企业
的评估分数,得其频率分布直方图如下:
(Ⅰ)估计该系统所属企业评估得分的中位数;
(Ⅱ)该系统要求各企业对照评分标准进行整改,若整改
后优秀企业数量不变,不合格企业、合格企业、良好企
业的数量依次成等差数列,系统所属企业获得贷款的均
值(即数学期望)不低于410万元,那么整改后不合格企
业占企业总数的百分比的最大值是多少?
 由Eξ≥410,得450-400a≥410,即a≤0.1.
(11分)
由Eξ≥410,得450-400a≥410,即a≤0.1.
(11分)
故整改后不合格企业占企业总数的百分比的最大值是10%. (12分)
15.(湖南师大附中2010届高三第五次月考试卷).某高三学生打算报名参加某7所高校中4所学校的自主招生考试,其中仅甲、乙两所学校的考试时间相同,因此该学生不能同时报考这两所学校,那么该学生不同的报考方法共有 25 种(用数字作答).
[解析]该学生若报考甲、乙两所学校中的1 所,则不同的报考方法共有 种;若不报考甲、乙两所学校,则不同的报考方法共有
种;若不报考甲、乙两所学校,则不同的报考方法共有 种.故该学生不同的报考方法共有20+5=25种.
种.故该学生不同的报考方法共有20+5=25种.
14.(湖南师大附中2010届高三第五次月考试卷)有一种掷正方体骰子走跳棋的网络游戏,棋盘上标有第0站,第1站,第2站,…,第100站.一枚棋子开始在第0站,玩家每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,则棋子向前跳一站;若掷出其余点数,则棋子向前跳两站. 游戏规定:若棋子经过若干次跳动恰跳到第99站,则玩家获胜,游戏结束;若棋子经过若干次跳动最后恰跳到第100站,则玩家失败,游戏结束.设棋子跳到第n站的概率为pn (n∈N,n≤100),可以证明: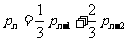 (2≤n≤100),则每次玩该游戏获胜的概率是
(2≤n≤100),则每次玩该游戏获胜的概率是
A. B.
B.  C.
C. 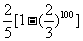 D.
D. 
解;由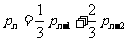 ,得
,得 .由已知,
.由已知,  ,
, ,
,
则数列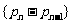 是首项为
是首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以 .
.
所以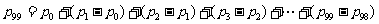
 .
.
所以玩该游戏获胜的概率是 ,故选A.
,故选A.
12.(北京市西城区2010年高三年级抽样测试)将编号为1、2、3的三个小球,放入编号为1、2、3、4的四个盒子中
如果每个盒子中最多放一个球,那么不同的放球方法有24, 种;
如果4号盒子中至少放两个球,那么不同的放球方法有 10 种。
13(北京市西城区2010年高三年级抽样测试)一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
4 |
5 |
 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元. 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求购买该商品的3位顾客中,至少有1位采用1期付款的概率;
(Ⅱ)求 的分布列及期望
的分布列及期望 .
.
解:(Ⅰ)设“购买该商品的3位顾客中至少有1位采用1期付款”为事件
“购买该商品的3位顾客中无人采用1期付款”为事件  -----------1分
-----------1分

 .
---------------- 6分
.
---------------- 6分
(Ⅱ) 的可能取值为
的可能取值为 元,
元, 元,
元, 元.
元.

 ,
,
 .
.
 的分布列为:
的分布列为:





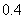
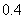
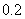

 (元). ---------------- 13分
(元). ---------------- 13分
11.(海淀区高三年级第一学期期末练习)某地区教研部门要对高三期中数学练习进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从所有试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
(Ⅰ)求样本试卷中该题的平均分,并据此估计这个地区高三学生该题的平均分;
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
解:(Ⅰ)设样本试卷中该题的平均分为 ,则由表中数据可得:
,则由表中数据可得:
 , ……………….4分
, ……………….4分
据此可估计这个地区高三学生该题的平均分为3.01分. ……………….5分
(Ⅱ)依题意,第一空答对的概率为0.8,第二空答对的概率为0.3,……………….7分
记“第一空答对”为事件 ,“第二空答对”为事件
,“第二空答对”为事件 ,则“第一空答错”为事件
,则“第一空答错”为事件 ,
“第二空答错”为事件
,
“第二空答错”为事件 .若要第一空得分不低于第二空得分,则
.若要第一空得分不低于第二空得分,则 发生或
发生或 与
与 同时发生,
同时发生,
……………….9分
故有:  . ……………….12分
. ……………….12分
答:该同学这道题第一空得分不低于第二空得分的概率为0.94. ……………….13分
10.(海淀区高三年级第一学期期末练习)某校在高二年级开设选修课,其中数学选修课开三个班.选课结束后,有四名同学要求改修数学,但每班至多可再接收2名同学,那么不同的分配方案有
A.72种 B.54种 C.36种 D.18种
9. (海淀区高三年级第一学期期末练习)先后两次抛掷一枚骰子,在得到点数之和不大于6的条件下,先后出现的点数中有3的概率为
A. B.
B. C.
C. D.
D.
8.(诸城市高三上学期1月数学试题)某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定
正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为 ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.
解:(I)记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过
决赛”为事件C,则 那么该选手在复赛阶段被淘汰的概率
那么该选手在复赛阶段被淘汰的概率
是 . ………………………………4分
. ………………………………4分
(II) 可能取值为1,2,3.
可能取值为1,2,3.

………………………………8分
 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
|
P |
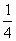 |
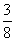 |
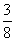 |
 的数学期望
的数学期望 ………………………………10分
………………………………10分
 的方差
的方差 . …………12分
. …………12分
7.(辽宁省锦州市2010届高三上学期期末考试)某食品企业一个月内被消费者投诉的次数用 表示,据统计,随机变量
表示,据统计,随机变量 的概率分布如下:
的概率分布如下:
 |
0 |
1 |
2 |
3 |
|
p |
0.1 |
0.3 |
2a |
a |
(Ⅰ)求a的值和 的数学期望;
的数学期望;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
解析:(1)由概率分布的性质有0.1+0.3+2a+a=1,解答a=0.2
 的概率分布为
的概率分布为
 |
0 |
1 |
2 |
3 |
|
P |
0.1 |
0.3 |
0.4 |
0.2 |
 (8分)
(8分)
(2)设事件A表示“两个月内共被投诉2次”事件 表示“两个月内有一个月被投诉2次,另外一个月被投诉0次”;事件
表示“两个月内有一个月被投诉2次,另外一个月被投诉0次”;事件 表示“两个月内每月均被投诉12次”
表示“两个月内每月均被投诉12次”
则由事件的独立性得

故该企业在这两个月内共被消费者投诉2次的概率为0.17 (14分)
6.(辽宁省锦州市2010届高三上学期期末考试)从某地区15000位老人中随机抽取500人,其生活能否自理的情况如下表所示:则该地区生活不能自理的老人中男性比女性约多__60____人.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com