
26.(宁波市2009学年度第一学期期末试卷)袋中装有编号为
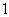 的球
的球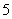 个,编号为
个,编号为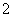 的球
的球 个,这些球的大小完全一样.
个,这些球的大小完全一样.
(1)从中任意取出四个,求剩下的四个球都是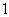 号球的概率;
号球的概率;
(2)从中任意取出三个,记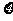 为这三个球的编号之和,
为这三个球的编号之和,
求随机变量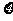 的分布列及其数
的分布列及其数 学期望
学期望 .
.
(1) 记 “任意取出四个, 剩下的四个球都是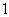 号球”为事件
号球”为事件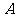 ,
,
则 ;
(4分)
;
(4分)
(2)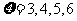
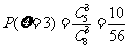 ,
,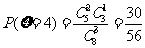 ,
,
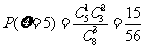 ,
, .
.
所以随机变量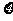 的分布列为
的分布列为

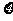
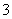
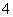
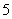

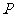
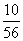
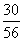
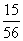
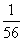


(12分)
 .
(14分)
.
(14分)
25.(2009-2010学年度扬州市第一学期期末高考模拟考试试题)若以连续掷两次骰子分 别得到的点数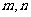 作为点
作为点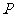 的横、
的横、
纵坐标,则点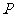 在直线
在直线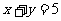 上的概率为 ▲
上的概率为 ▲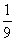 .
.
24.(2009-2010学年度扬州市第一学期期末高考模拟考试试题)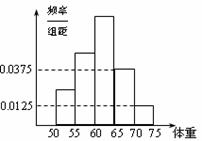 如图是某学校学生体重的频率分布直方图,已知图中
如图是某学校学生体重的频率分布直方图,已知图中
从左到右的前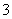 个小组的频率之比为
个小组的频率之比为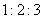 ,第
,第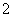 小组
小组
的频数为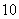 ,则抽取的学生人数是
▲
,则抽取的学生人数是
▲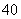 .
.
23.(江苏省苏东三市高三数学调研试卷)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有
80人.为了调查职工的健康状况,用分层抽样的方法从全体职工中抽取一个容量为25的样本,应抽取超过45岁的职工___▲_____人.
22.(2010年浙江省杭州市第一次高考科目教学质量检测数学理科卷)某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(Ⅰ)当A、D区域同时用红色鲜花时,求布置花圃的不同方法的种数;

(第21题)
(Ⅱ)求恰有两个区域用红色鲜花的概率;
(Ⅲ)记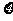 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量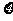 的分布列及其数学期望E
的分布列及其数学期望E .
.
(Ⅰ)当A、D区域同时用红色鲜花时,其它区域不能用红色.
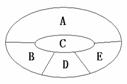
(第21题)
因此,布置花圃的不同方法的种数为4´3´3 = 36种.… ………………4分
(穷举全部情况满分,部分情况酌情给分)
(Ⅱ)设M表示事件“恰有两个区域用红色鲜花”,
当区域A、D同色时,共有 种;
种;
当区域A、D不同色时,共有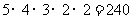 种;
种;
因此,所有基本事件总数为:180+240=420种(是等可能的)……2分
又因为A、D为红色时,共有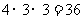 种;
种;
B、E为红色时,共有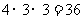 种;
种;
因此,事件M包含的基本事件有:36+36=72种.
所以,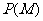 =
=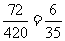 .
……………………………………………3分
.
……………………………………………3分
(Ⅲ)随机变量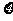 的分布列为:
的分布列为:
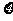 |
0 |
1 |
2 |
|
P |
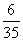 |
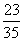 |
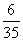 |
所以, =
=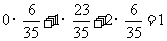 .……………………………………6分
.……………………………………6分
21.(2010年浙江省杭州市第一次高考科目教学质量检测数学理科卷)《中华人民共和国个人所得税法》规定,公
民全月工资、薪金所得不超过2000元的不必纳
|
全月应纳税所得额 |
税率 |
|
不超过500元的部分 |
5% |
|
超过500元至2000元的部分 |
10% |
|
超过2000元至5000元的部分 |
15% |
|
…… |
… |
税,超过2000元的部分为全月应纳税所得额.
此项税款按下表分段累进计算: 某人一月份应
某人一月份应
交纳此项税款135元,则他的当月工资、薪金
的税后所得是 3465 元.
20.(2010年浙江省杭州市第一次高考科目教学质量检测数学理科卷)从某市参加高中数学建模竞赛的1008份试卷中随机抽取一个容量为54的样本,考查竞赛的成绩分布,将样本分成6组,绘成频率分布直方图(如图),从左到右各小组的小矩形的高的比为1:1:4:6:4:2. 据此估计该市在这次竞赛中,成绩高于85分的学生总人数为 224
人
19.(湖北省部分重点中学2010届高三第二次联考)袋中有大小相同的5个球,其中黑球3个,白球2个,甲乙二人分别从中各取一个,甲先取(不放回)乙后取。
(1)分别求甲乙取到黑球的概率;(2)求两人共取到黑球的个数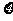 的数学期望。
的数学期望。
解:(1)记“甲取到黑球”为事件A,“乙取到黑球为事件B”
则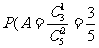 …………3分
…………3分
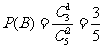 故甲、乙取到黑球的概率均为
故甲、乙取到黑球的概率均为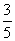 …………6分
…………6分
(2)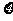 的所有可能取值为0,1,2
的所有可能取值为0,1,2
且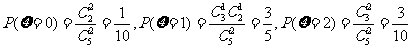
∴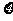 的分布列为
的分布列为
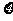 |
0 |
1 |
2 |
|
P |
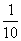 |
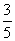 |
 |
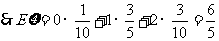
(注意:错误算法的答案也是 ) …………12分
) …………12分
18.(湖北省部分重点中学2010届高三第二次联考)北京大学今年实施校长实名推荐制,某中学获得推荐4名学生的资格,校长要从7名优秀学生中推荐4名,7名学生中有2人有体育特长,另有2人有艺术特长,其余3人有其他特长,那么至少含有一名有体育特长和一名有艺术特长的学生的推荐方案有 25 种(用数字作答)。
17.(广东省广州市2010届高三上学期期末调研)某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(1)设所选3人中女生人数为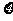 ,求
,求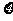 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
(1)解: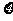 的所有可能取值为0,1,2.…………………………1分
的所有可能取值为0,1,2.…………………………1分
依题意,得 ,
,
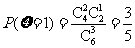 ,
, 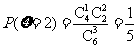 .
.
∴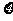 的分布列为
的分布列为
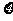 |
0 |
1 |
2 |
||
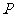 |
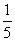 |
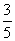 |
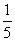
|
∴ 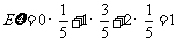 .…………………………………………………6分
.…………………………………………………6分
(2)解法1:设“男生甲被选中”为事件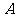 ,“女生乙被选中”为事件
,“女生乙被选中”为事件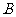 ,
,
 则
则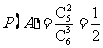 ,
, , ………………………………………10分
, ………………………………………10分
∴ .
.
故在男生甲被选中的情况下,女生乙也被选中的概率为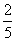 .……………………12分
.……………………12分
解法2:设“男生甲被选中的情况下,女生乙也被选中”为事件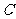 ,
,
从4个男生、2个女生中选3人,男生甲被选中的种数为 ,…………………………………8分
,…………………………………8分
男生甲被选中,女生乙也被选中的种数为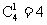 ,………………………………10分
,………………………………10分
∴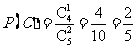 .
.
故在男生甲被选中的情况下,女生乙也被选中的概率为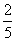 .………………………12分
.………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com