
19. 真空中Ox坐标轴上的某点有一个点电荷Q,坐标轴上A、B两点的坐标分别为0.2m和0.7m。在A点放一个带正电的试探电荷,在B点放一个带负电的试探电荷,A、B两点的试探电荷受到电场力的方向都跟x轴正方向相同,电场力的大小F跟试探电荷电量q的关系分别如图中直线a、b所示。下列说法正确的是
真空中Ox坐标轴上的某点有一个点电荷Q,坐标轴上A、B两点的坐标分别为0.2m和0.7m。在A点放一个带正电的试探电荷,在B点放一个带负电的试探电荷,A、B两点的试探电荷受到电场力的方向都跟x轴正方向相同,电场力的大小F跟试探电荷电量q的关系分别如图中直线a、b所示。下列说法正确的是
A.B点的电场强度的大小为0.25N/C
B.A点的电场强度的方向沿x轴负方向
C.点电荷Q是正电荷
D.点电荷Q的位置坐标为0.3m
18.我国的“神舟七号”飞船于2008年9月25日晚9时10分载着3名宇航员顺利升空,并成功“出舱”和安全返回地面。当“神七”在绕地球做半径为r的匀速圆周运动时,设飞船舱内质量为m的航天员站在可称体重的台秤上。用R表示地球的半径,g表示地球表面处的重力加速度,g´表示飞船所在处的重力加速度,N表示航天员对台秤的压力,则下列关系式中正确的是
A.g´=0
B.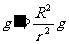 C.N=mg D.
C.N=mg D.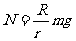
17.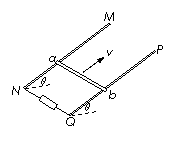 如图所示,两根足够长的光滑金属导轨MN、PQ平行放置,导轨平面的倾角为θ,导轨的下端接有电阻。当空间没有磁场时,使ab以平行导轨平面的初速度v0冲上导轨平面,ab上升的最大高度为H;当空间存在垂直导轨平面的匀强磁场时,再次使ab以相同的初速度从同一位置冲上导轨平面,ab上升的最大高度为h。两次运动中导体棒ab始终与两导轨垂直且接触良好。关于上述情景,下列说法中正确的是
如图所示,两根足够长的光滑金属导轨MN、PQ平行放置,导轨平面的倾角为θ,导轨的下端接有电阻。当空间没有磁场时,使ab以平行导轨平面的初速度v0冲上导轨平面,ab上升的最大高度为H;当空间存在垂直导轨平面的匀强磁场时,再次使ab以相同的初速度从同一位置冲上导轨平面,ab上升的最大高度为h。两次运动中导体棒ab始终与两导轨垂直且接触良好。关于上述情景,下列说法中正确的是
A.两次上升的最大高度比较,有H=h
B.两次上升的最大高度比较,有H<h
C.有磁场时,ab上升过程的最大加速度为gsinθ
D.有磁场时,ab上升过程的最小加速度为gsinθ
16. 如图1所示,一根水平张紧弹性长绳上有等间距的O、P、Q质点,相邻两质点间距离为1.0m。t=0时刻O质点从平衡位置开始沿y轴方向振动,并产生沿x轴正方向传播的波,O质点的振动图象如图2所示,当O质点第一次达到正方向最大位移时刻,P质点刚开始振动,则
如图1所示,一根水平张紧弹性长绳上有等间距的O、P、Q质点,相邻两质点间距离为1.0m。t=0时刻O质点从平衡位置开始沿y轴方向振动,并产生沿x轴正方向传播的波,O质点的振动图象如图2所示,当O质点第一次达到正方向最大位移时刻,P质点刚开始振动,则
A.O、P两质点之间的距离为半个波长
|
C.这列波传播的速度为1.0m/s
D.在一个周期内,O质点通过的路程为4.0m
15.如图所示,把电感线圈L、电容器C、电阻R分别与灯泡L1、L2、L3串联后接在交流电源两极间,三盏灯亮度相同。若保持交流电源两极间的电压不变,使交流电的频率增大,则以下判断正确的是
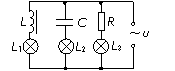 A.与线圈L连接的灯泡L1将变暗
A.与线圈L连接的灯泡L1将变暗
B.与电容器C连接的灯泡L2将变暗
C.与电阻R连接的灯泡L3将变暗
D.三盏灯的亮度都不会改变
14. 一束可见光a由三种单色光m、p、n组成。光束a通过三棱镜后情况如图所示,检测发现单色光p能使某金属产生光电效应,下列叙述正确的是
一束可见光a由三种单色光m、p、n组成。光束a通过三棱镜后情况如图所示,检测发现单色光p能使某金属产生光电效应,下列叙述正确的是
A.真空中单色光m的波长大于n的波长
B.单色光m的频率大于n的频率
C.单色光n一定可以使该金属发生光电效应
D.在三棱镜中,单色光m的光速大于n的光速
13.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步。下列表述正确的是
A.牛顿发现了万有引力定律 B.洛伦兹发现了电磁感应定律
C.α粒子散射现象表明了原子核有复杂结构 D.狭义相对论认为运动物体的质量与速度无关
20.(1)由 可得
可得 ,两式相减得
,两式相减得
又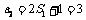 ∴
∴ 故{an}是首项为1,公比为3得等比数列 ∴
故{an}是首项为1,公比为3得等比数列 ∴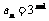 . 6分
. 6分
(2)设{bn}的公差为d,由 得,可得
得,可得 ,可得
,可得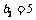 ,
,
故可设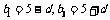
又 由题意可得
由题意可得 解得
解得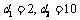

∵等差数列{bn}的各项为正,∴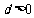 ,∴
,∴ ∴
∴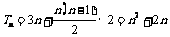 12分
12分
(i)


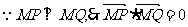 ,
,
故得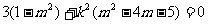 对任意的
对任意的
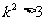 恒成立,
恒成立,
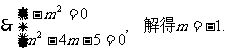
∴当m =-1时,MP⊥MQ. 10分
当直线l的斜率不存在时,由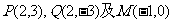 知结论也成立,
知结论也成立,
综上,当m =-1时,MP⊥MQ. ……………………………………………………12分
22解:(Ⅰ)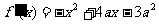 (1分)
(1分)
令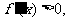 得
得 的单调递增区间为(a,3a)
的单调递增区间为(a,3a)
令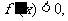 得
得 的单调递减区间为(-
的单调递减区间为(- ,a)和(3a,+
,a)和(3a,+ ) (4分)
) (4分)
∴当x=a时, 极小值=
极小值=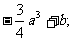
当x=3a时, 极小值=b. (6分)
极小值=b. (6分)
(Ⅱ)由| |≤a,得-a≤-x2+4ax-3a2≤a.①(7分)
|≤a,得-a≤-x2+4ax-3a2≤a.①(7分)
∵0<a<1,
∴a+1>2a.
∴ 上是减函数. (9分)
上是减函数. (9分)
∴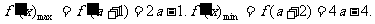
于是,对任意 ,不等式①恒成立,等价于
,不等式①恒成立,等价于

又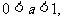
∴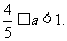 12分
12分
19.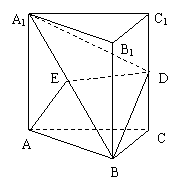 解: (Ⅰ)取AB中点G,连结EG.
解: (Ⅰ)取AB中点G,连结EG.
∵E为A1B中点,
∵EG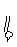
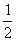 A1A,
A1A,
且EG=a;
又∵D为C1C中点,
∴DC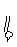 EG,
EG,
∴CDEG为平行四边形,
∴DE∥CG,而CG 面ABC,DE
面ABC,DE 面ABC,
面ABC,
∴DE∥平面ABC. 4分
(Ⅱ)由已知有CG⊥AB,A1A⊥平面ABC,CG 面ABC.
面ABC.
∴A1A⊥CG,
∴CG⊥平面ABA1.
又∵DE∥CG,
∴DE⊥平面ABA1,而且AE 面ABA1,
面ABA1,
∴DE⊥AE.
又∵AE⊥A1B,而DE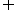 A1B,
A1B,
∴AE⊥平面BDA1.∴AE⊥BD. 8分
(Ⅲ)∵DE⊥平面ABA1,]
∴
由已知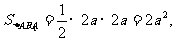
在正△ABC中,CG=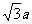 ,∴DE=
,∴DE=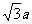 .
.
∴ 12分
12分
20.(本小题满分12分)
数列{an}的前n项和记为Sn,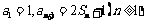
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且 ,又
,又 成等比数列,求Tn
成等比数列,求Tn
21 (本小题满分12分)已知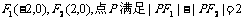 ,记点P的轨迹为E.
,记点P的轨迹为E.
(1)求轨迹E的方程;
(2)若直线l过点F2且与轨迹E交于P、Q两点.
(i)无论直线l绕点F2怎样转动,在x轴上总存在定点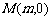 ,使
,使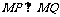 恒成立,求实数m的值.
恒成立,求实数m的值.
22 (本小题满分12分).设函数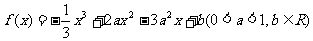 .
.
(Ⅰ)求函数f(x)的单调区间和极值;
(Ⅱ)若对任意的 不等式|
f′(x)|≤a恒成立,求a的取值范围.
不等式|
f′(x)|≤a恒成立,求a的取值范围.
文科3,20答案

一 选择题 CADDB ACCBA DD
当 ,即
,即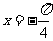 时,
时, 有最小值
有最小值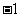 . ………12分
. ………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com