
6、如右图所示,定义在D上的函数 ,如果满足:对
,如果满足:对 ,
,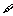 常数A,都有
常数A,都有 成立,则称函数
成立,则称函数 在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
(1)试判断函数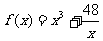 在
在 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(2)已知某质点的运动方程为 ,要使在
,要使在 上的每一时刻
上的每一时刻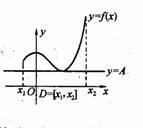 该质点的瞬时速度是以
该质点的瞬时速度是以 为下界的函数,求实数a的取值范围.
为下界的函数,求实数a的取值范围.
解:1)求导或基本不等式的推广都可以证明有下界(A=32)存在.
(2)质点在 上的每一时刻该质点的瞬时速度
上的每一时刻该质点的瞬时速度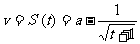 。
。
依题意得对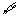
 有
有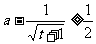
即: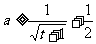 对
对
 恒成立 .所以
恒成立 .所以 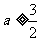 .
.
5、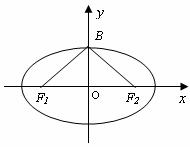 如图,已知椭圆
如图,已知椭圆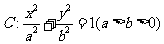 的焦点和上顶点分别为
的焦点和上顶点分别为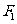 、
、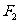 、
、 ,我们称
,我们称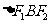 为椭圆
为椭圆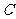 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为 椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为 椭圆的相似比.
(1)已知椭圆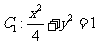 和
和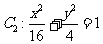 ,判断
,判断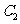 与
与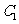 是否相似,如果相似则求出
是否相似,如果相似则求出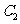 与
与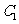 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)已知直线 ,与椭圆
,与椭圆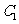 相似且半短轴长为
相似且半短轴长为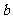 的椭圆
的椭圆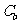 的方程,
的方程,
在椭圆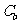 上是否存在两点
上是否存在两点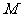 、
、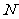 关于直线
关于直线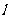 对称,若存在,则求出函数
对称,若存在,则求出函数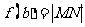 的解析式.
的解析式.
(3)根据与椭圆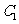 相似且半短轴长为
相似且半短轴长为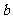 的椭圆
的椭圆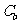 的方程,提出你认为有价值的
相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的
相似椭圆之间的三种性质(不需证明);
、解:(1)椭圆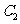 与
与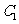 相似. ………2分
相似. ………2分
因为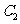 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为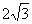 的等腰三角形,
的等腰三角形,
而椭圆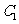 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为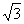 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为 ……… 6分
……… 6分
(2)椭圆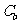 的方程为:
的方程为: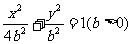 .
……8分
.
……8分
假定存在,则设 、
、 所在直线为
所在直线为 ,
,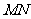 中点为
中点为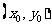 .
.
则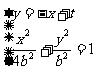
 .
………10分
.
………10分
所以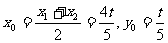 .
.
中点在直线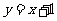 上,所以有
上,所以有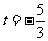 .
.
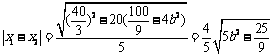 .
.
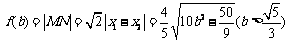 .
.
(3)椭圆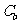 的方程为:
的方程为: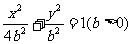 .
.
两个相似椭圆之间的性质有:
两个相似椭圆的面积之比为相似比的平方;
① 分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
② 两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比.
4、若有穷数列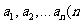 是正整数),满足
是正整数),满足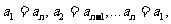 即
即 (
(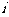 是正整数,且
是正整数,且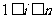 )就称该数列为“对称数列”
)就称该数列为“对称数列”
(I)
已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且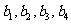 成等差数列,
成等差数列,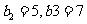 试写出
试写出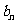 的每一项;
的每一项;
(II)
已知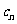 是项数
是项数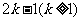 的对称数列,且
的对称数列,且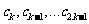 构成首项为70,公差为-4的等差数列,数列
构成首项为70,公差为-4的等差数列,数列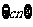 的前
的前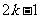 项和为
项和为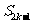 取到最大值并求此最大值;
取到最大值并求此最大值;
(III)
对于给定的正整数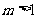 ,试写出所有项数不超过
,试写出所有项数不超过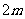 的对称数列,使得1,2,22,……2m-1称谓数列中的连续项;当
的对称数列,使得1,2,22,……2m-1称谓数列中的连续项;当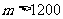 ,试求其中该数列的前2009项的和
,试求其中该数列的前2009项的和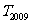
解(I)设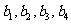 公差为
公差为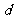 ,由
,由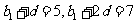 得
得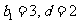
 数列
数列 为3,5,7,9,7,5,3,……2分
为3,5,7,9,7,5,3,……2分
(II) ……3分
……3分
又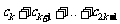 =
=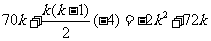 ……4分
……4分
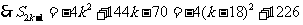
(III)所有可能的“对称数列”是①1,2,22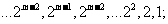
②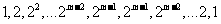
③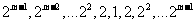
④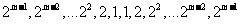 ……9分
……9分
当
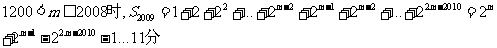
对于②当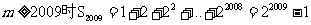
当
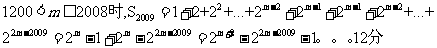
对于③当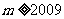 时,
时,
当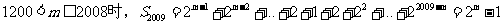
 分
分
对于④当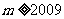 时,
时,
当
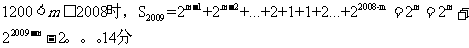
3、如果对任意一个三角形,只要它的三边长a,b,c都在函数f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.
 (1)判断下列函数是不是“保三角形函数”,并证明你的结论:
(1)判断下列函数是不是“保三角形函数”,并证明你的结论:
① f(x)= ; ② g(x)=sinx (x∈(0,π)).
(2)若函数h(x)=lnx (x∈[M,+∞))是保三角形函数,求M的最小值.
(1)[答]f(x)= 是保三角形函数,g(x)=sinx (x∈(0,π))不是保三角形函数.
[证明]① f(x)= 是保三角形函数.
对任意一个三角形的三边长a,b,c,则a+b>c,b+c>a,c+a>b,
f(a)= ,f(b)= ,f(c)= .
因为(+)2=a+2+b>c+2>()2,所以+>.
同理可以证明:+>,+>.
所以f(a)、f(b)、f(c)也是某个三角形的三边长,故 f(x)= 是保三角形函数. ………………4分
②g(x)=sinx (x∈(0,π))不是保三角形函数. 取 ,显然这三个数能作为一个
,显然这三个数能作为一个
三角形的三条边的长. 而sin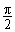 =1,sin
=1,sin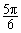 =,不能作为一个三角形的三边长.
=,不能作为一个三角形的三边长.
所以g(x)=sinx (x∈(0,π))不是保三角形函数.……………8分
(2)[解]M的最小值为2. ………… 10分
(i)首先证明当M≥2时,函数h(x)=lnx (x∈[M,+∞))是保三角形函数.
对任意一个三角形三边长a,b,c∈[M,+∞),且a+b>c,b+c>a,c+a>b,
则h(a)=lna,h(b)=lnb,h(c)=lnc.
因为a≥2,b≥2,a+b>c,所以(a-1)(b-1)≥1,所以ab≥a+b>c,所以lnab>lnc,
即lna+lnb>lnc.
同理可证明lnb+lnc>lna,lnc+lna>lnb.
所以lna,lnb,lnc是一个三角形的三边长.
故函数h(x)=lnx (x∈[M,+∞),M≥2),是保三角形函数. ……… 13分
(ii)其次证明当0<M<2时,h(x)=lnx (x∈[M,+∞))不是保三角形函数.
当0<M<2时,取三个数M,M,M2∈[M,+∞),
因为0<M<2,所以M+M=2M>M2,所以M,M,M2是某个三角形的三条边长,
而lnM+lnM=2lnM=lnM2,所以lnM,lnM,lnM2不能为某个三角形的三边长,所以h(x)=lnx 不是保三角形函数.
所以,当M<2时,h(x)=lnx (x∈[M,+∞))不是保三角形函数.
综上所述:M的最小值为2. ………… 16分
1、已知函数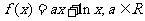
(I)求函数 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点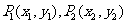 ,如果存在曲线上的点
,如果存在曲线上的点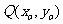 ,且
,且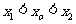 ,使得曲线在点
,使得曲线在点 处的切线
处的切线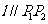 ,则称
,则称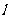 为弦
为弦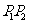 的伴随切线,特别地,当
的伴随切线,特别地,当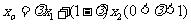 时,又称
时,又称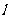 为
为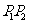 的
的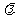 伴随切线。
伴随切线。
(i)求证:曲线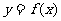 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ii)是否存在曲线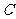 ,使得曲线
,使得曲线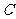 的任意一条弦均有
的任意一条弦均有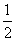 伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由。
伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由。
解法一:
(I)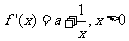 当
当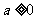 时,
时,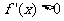 ,函数
,函数 在
在 内是增函数,
内是增函数,
 函数
函数 没有极值
没有极值
当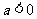 时,令
时,令 得
得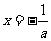
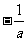
当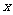 变化时,
变化时, 与
与 变化情况如下表:
变化情况如下表:
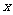 |
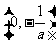 |
 |
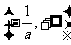 |
 |
+ |
0 |
- |
 |
单调递增 |
极大值 |
单调递减 |
 当
当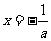 时,
时, 取得极大值
取得极大值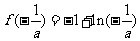
综上,当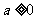 时,
时, 没有极值;
没有极值;
当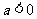 时,
时, 的极大值为
的极大值为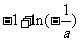 ,没有极小值
,没有极小值
(Ⅱ)(i)设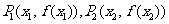 是曲线
是曲线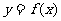 上的任意两点,要证明
上的任意两点,要证明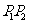 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点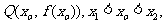 使得
使得
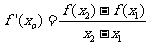 ,且点
,且点 不在
不在 上。
上。
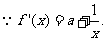 即证存在
即证存在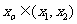 ,使得
,使得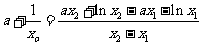
即 成立,且点
成立,且点 不在
不在 上
上
以下证明方程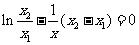 在
在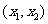 内有解。
内有解。
记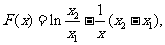 则
则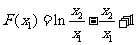
令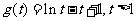
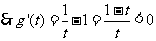
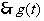 在
在 内是减函数,
内是减函数,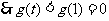
取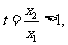 则
则 ,即
,即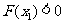
同理可证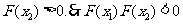
 函数
函数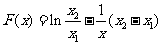 在(
在(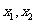 )内有零点
)内有零点
即方程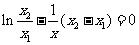 在
在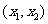 内有解
内有解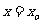
又对于函数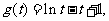 取
取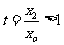 ,则
,则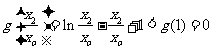 ,
,
可知 即点
即点 不在
不在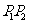 上。
上。
又 是增函数,
是增函数,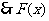 的零点是唯一的,
的零点是唯一的,
即方程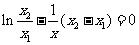 在
在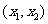 内有唯一解
内有唯一解
综上,曲线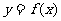 上的任意一条弦均有伴随切线,并且伴随切线是唯一的
上的任意一条弦均有伴随切线,并且伴随切线是唯一的
(ii)取曲线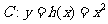 ,则曲线
,则曲线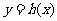 的任意一条弦均有
的任意一条弦均有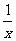 伴随切线。
伴随切线。
证明如下:
设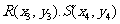 是曲线
是曲线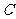 上任意两点
上任意两点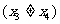 ,
,
则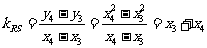
即曲线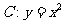 的任意一条弦均有
的任意一条弦均有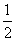 伴随切线
伴随切线
注:只要考生给出一条满足条件的曲线,并给出正确证明,均给满分,若只给
曲线,没有给出正确的证明,不给分。
解法二:
(I)同解法一。
(Ⅱ)(i)设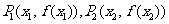 是曲线
是曲线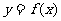 上的任意两点,要证明
上的任意两点,要证明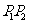 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点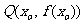 ,
,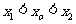 ,使得
,使得
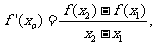 且点
且点 不在
不在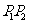 上
上
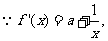 即证存在
即证存在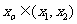 ,使得
,使得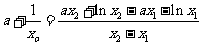
即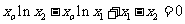 成立,且点
成立,且点 不在
不在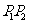 上
上
以下证明方程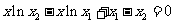 在
在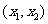 内有解
内有解
设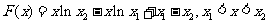
则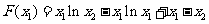
记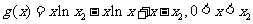
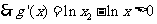
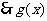 在
在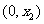 内是增函数,
内是增函数,
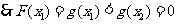
同理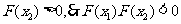
 方程
方程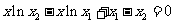 在
在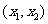 内有解
内有解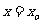
又对于函数

可知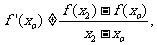 即点
即点 不在
不在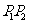 上。
上。
又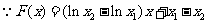 在
在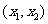 内是增函数。
内是增函数。
 方程
方程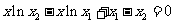 在
在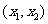 内有唯一解
内有唯一解
综上,曲线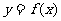 上的任意一条弦均有伴随切线,并且伴随切线是唯一的
上的任意一条弦均有伴随切线,并且伴随切线是唯一的
(ii)同解法一。
2下述数阵称为“森德拉姆筛”,记为S.其特点是每行每列都是等差数列,第i行第j列的数记为 Aij.
Aij.
 1 4 7 10 13 …
1 4 7 10 13 …
 4 8 12 16 20 …
4 8 12 16 20 …
 7 12 17 22 27 …
7 12 17 22 27 …
 10 16 22 28 34 …
10 16 22 28 34 …
 13 20 27 34 41 …
13 20 27 34 41 …
 … … … …
… … … …

 (1)证明:存在常数
(1)证明:存在常数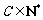 ,对任意正整数i、j,
,对任意正整数i、j,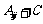 总是合数;
总是合数;
 (2)设 S中主对角线上的数1,8,17,28,41,…组成数列
(2)设 S中主对角线上的数1,8,17,28,41,…组成数列 . 试证不存在正整数k和m
. 试证不存在正整数k和m
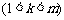 ,使得
,使得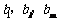 成等比数列;
成等比数列;
 (3)对于(2)中的数列
(3)对于(2)中的数列 ,是否存在正整数p和r
,是否存在正整数p和r 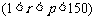 ,使得
,使得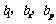 成等差数列.若存在,写出
成等差数列.若存在,写出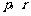 的一组解(不必写出推理过程);若不存在,请说明理由.
的一组解(不必写出推理过程);若不存在,请说明理由.
(1)[证明]因为第一行数组成的数列{A1j}(j=1,2,…)是以1为首项,公差为3的等差数列,所以A1 j=1+(j-1)×3=3 j-2,
第二行数组成的数列{A2j}(j=1,2,…)是以4为首项,公差为4的等差数列,
所以A2 j=4+(j-1)×4=4j ………………………2分
所以A2 j-A1 j=4 j-(3 j-2)=j+2,
所以第j列数组成的数列{ Aij}(i=1,2,…)是以3 j-2为首项,
公差为 j+2的等差数列,
所以Aij=3 j-2+(i-1) ×(j+2) =ij+2i+2j-4
=(i+3) (j+2) 8. ……………5分
故Aij+8=(i+3) (j+2)是合数.
所以当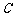 =8时,对任意正整数i、j,
=8时,对任意正整数i、j,
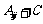 总是合数
…………6分
总是合数
…………6分
(2)[证明](反证法)假设存在k、m,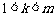 ,使得
,使得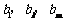 成等比数列,即
成等比数列,即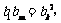 ……………7分
……………7分
∵bn=Ann =(n+2)2-4
∴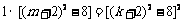
得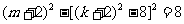 ,
,
即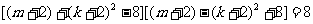 ,
10分
,
10分
又∵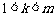 ,且k、m∈N,∴k≥2、m≥3,
,且k、m∈N,∴k≥2、m≥3,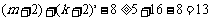
∴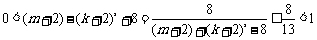 ,这与
,这与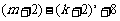 ∈Z矛盾,所以不存在正整数k和m
∈Z矛盾,所以不存在正整数k和m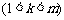 ,
,
使得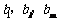 成等比数列.……………12分
成等比数列.……………12分
(3)[解]假设存在满足条件的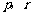 ,那么
,那么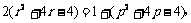
即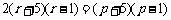 . ……… 14分
. ……… 14分
不妨令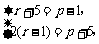 得
得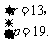
所以存在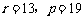 使得
使得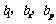 成等差数列. …… 16分
成等差数列. …… 16分
(注:第(3)问中数组 不唯一,例如
不唯一,例如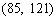 也可以)
也可以)
17、设函数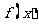 的定义域为
的定义域为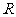 ,若存在常数
,若存在常数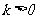 ,使
,使
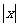 对一切实数
对一切实数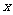 均成立,则称
均成立,则称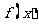 为“海宝”函数. 给出下列函数:
为“海宝”函数. 给出下列函数:
①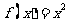 ;②
;②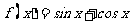 ;③
;③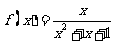 ;④
;④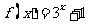
 其中
其中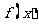 是“海宝”函数的序号为 ③ .
是“海宝”函数的序号为 ③ .
16、定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和. 已知数列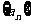 是等和数列, 且a1=2,
公和为5,那么a18的值为 3, ,且这个数列的前21项和S21的值为 52 .
是等和数列, 且a1=2,
公和为5,那么a18的值为 3, ,且这个数列的前21项和S21的值为 52 .
15、若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有__9_____个
14.给出定义:若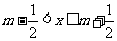 (其中
(其中 为整数),则
为整数),则 叫做离实数
叫做离实数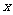 最近的整数,记作
最近的整数,记作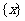 ,即
,即
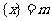 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数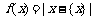 的四个命题:
①函数
的四个命题:
①函数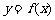 的定义域是R,值域是[0,
的定义域是R,值域是[0,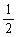 ];
];
②函数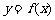 的图像关于直线
的图像关于直线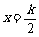 (k∈Z)对称;
(k∈Z)对称;
③函数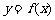 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④ 函数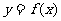 在
在 上是增函数;
上是增函数;

则其中真命题是__①②③ .
13、第29届奥运会在北京举行.设数列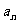 =
=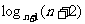
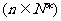 ,定义使
,定义使 为整数的实数k为奥运吉祥数,则在区间[1,2008]内的所有奥运吉祥数之和为____
为整数的实数k为奥运吉祥数,则在区间[1,2008]内的所有奥运吉祥数之和为____ 2026____.
2026____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com