
14、下列各句中,有语病的一句是(3分)
A、在当前国际金融危机背景下,我国应当有效利用知识产权制度功效,充分发挥知识产权的政策导向,尤其是加大政府对创新的支持力度。
B、为科学有序地做好教育系统甲型HINI流感疫情防控工作,提高防控和应对甲型HINI流感的能力,教育部、卫生部联合印发《学校甲型HINI流感防控工作(方案试行)》。
C、近年来,媒体揭露高考作弊的新闻,保护了广大考生的合法权益,给予种种不法行为以强有力的震慑。
D、为方便农村群众看病就医,特别是为解决偏远地方缺医少药、农民“看病难,看病贵”的问题 ,今年10月,我市卫生局深入农村开展巡回医疗服务活动。
13、下列各句中,加点的成语使用不恰当的一项是(3分)
A、这类文章涉及的知识面广,知识领域多,往往令读者目不暇接。
B、王老师当班主任30年,勤勤恳恳,日理万机,积劳成疾还坚持工作。
C、一些业内人士认为,这次庆祝建国60周年暨“红歌唱响六盘山 ”万人歌咏大会从舞台布景、乐队伴奏到电视表现手法等等,都加入了很多现代元素,使得新时代的红歌能够做到老少皆宜,雅俗共赏。
D、洪都拉斯发生政变时,总统塞拉亚穿着睡衣被拘捕的消息不胫而走,世界各国的广播、电视、报纸、网络等媒体纷纷在第一时间报道了这一突发性新闻。
8、对于定义域为 的函数
的函数 ,若同时满足:①
,若同时满足:① 在
在 内单调递增或单调递减;②存在区间[
内单调递增或单调递减;②存在区间[ ]
]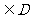 ,使
,使 在
在 上的值域为
上的值域为 ;那么把函数
;那么把函数 (
(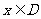 )叫做闭函数.
)叫做闭函数.
(1) 求闭函数 符合条件②的区间
符合条件②的区间 ;
;
(2) 若 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.
解:(1)由题意,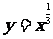 在[
在[ ]上递增,则
]上递增,则 ,----1分
,----1分
解得 或
或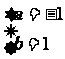 或
或 .
.
所以,所求的区间为[-1,0]或[-1,1]或[0,1] .
(2)若 是闭函数,则存在区间[
是闭函数,则存在区间[ ],在区间[
],在区间[ ]上,函数
]上,函数 的值域为[
的值域为[ ].
].
容易证明函数 在定义域内单调递增,
在定义域内单调递增,
∴  .
.
∴  为方程
为方程 的两个实数根.
的两个实数根.
即方程 有两个不相等的实根.
有两个不相等的实根.
 .(少1个式子扣1分)
.(少1个式子扣1分)
解得: ,综上所述,
,综上所述,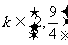 .
.

7、已知函数 自变量取值区间
自变量取值区间 ,若其值域区间也为
,若其值域区间也为 ,则称区间
,则称区间 为
为 的保值区间.
的保值区间.
(Ⅰ)求函数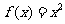 形如
形如 的保值区间;
的保值区间;
(Ⅱ) 的保值区间是
的保值区间是 ,求
,求 的取值范围.
的取值范围.
解:(Ⅰ)若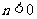 ,则
,则 ,矛盾.
,矛盾.
若 ,则
,则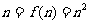 ,解得
,解得 或1
或1
所以 的保值区间为
的保值区间为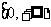 或
或 分
分
(Ⅱ)因为 的保值区间是
的保值区间是 ,
,
所以 ,即
,即
 ,得
,得
所以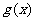 在
在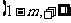 上为增函数,同理可得
上为增函数,同理可得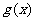 在
在 上为减函数…10分
上为减函数…10分
若 即
即 时,
时, 得
得 满足题意
满足题意
若 时,
时,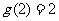 ,
,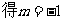 ,矛盾。
,矛盾。
所以满足条件的 值为
值为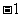
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com