
3.右边是一个算法的程序框图,当输入的 值为2009时,
值为2009时,
输出 的结果恰好是
的结果恰好是 ,则“?”处的关系式是
,则“?”处的关系式是
A. B.
B. C.
C. D.
D.
2.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现反面朝上的概率是
 A.
A. B.
B. C.
C. D.
D.
1. 现要完成下列3项抽样调查:
①从15瓶饮料中抽取5瓶进行食品卫生检查.
②台州某中学共有240名教职工,其中一般教师180名,行政人员24名,后勤人员36名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.
③科技报告厅有25排,每排有38个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请25名听众进行座谈.
较为合理的抽样方法是
A.①简单随机抽样, ②系统抽样, ③分层抽样
B.①简单随机抽样, ②分层抽样, ③系统抽样
C.①系统抽样, ②简单随机抽样, ③分层抽样
D.①分层抽样, ②系统抽样, ③简单随机抽样
17.请联系全文,谈谈“这株小花和这只小昆虫,它们的生和死浇铸的那尊雕像”为什么使作者如此刻骨铭心?(6分)
16.第六段在描写大兴安岭的春天来临时,运用了什么表现手法?有什么作用?试举例分析。(6分)
15.结合上下文,简要回答下面问题。(6分)
(1)“在那里,春天似乎还在遥远的地方逡巡”这句话中,“似乎”有什么含义?
(2)“现在,我知道,春天其实是由万物经过艰苦的甚至于牺牲抗争迎来的。”请从文中举例说明。
14.第二段描写冻土原上的严冬有什么作用?(4分)
21. 解:(1)将点 代入
代入 中得
中得
 ,所以
,所以 ,数列
,数列 为以6为首项,1为公差的等差数列.
为以6为首项,1为公差的等差数列.
 .……3分
.……3分
因为点 在直线
在直线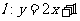 上,所以
上,所以 . ……4分
. ……4分
(2)由(1)得 ……5分
……5分
当k为偶数时,k+27为奇数,
 ,k=4. ……6分
,k=4. ……6分
当k为奇数时,k+27为偶数,
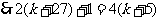 ,解得
,解得 (舍去) ……7分
(舍去) ……7分
综上,存在唯一的k=4答条件. ……8分
(3)由
即 ……9分
……9分
记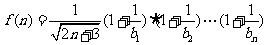 ……10分
……10分


= ;
;
所以 ,即
,即 是单调递增数列, ……12分
是单调递增数列, ……12分


故 的取值范围是
的取值范围是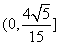 ……14分
……14分
20.解:(1)当 时,
时,
 , ……1分
, ……1分
∴当 时,
时, ,此时
,此时 单调递减
单调递减
当 时,
时,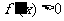 ,此时
,此时 单调递增 …………………………………3分
单调递增 …………………………………3分
 的的单调递减区间为(0,1);单调递增区间为(1,e);
的的单调递减区间为(0,1);单调递增区间为(1,e);
 的极小值为
的极小值为 ………………………………………………4分
………………………………………………4分
(2)由(1)知 在
在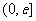 上的最小值为1,
……………………………………5分
上的最小值为1,
……………………………………5分
令 ,
,
 , ………………………6分
, ………………………6分
当 时,
时, ,
, 在
在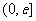 上单调递增
…………………………………7分
上单调递增
…………………………………7分
∴
∴在(1)的条件下, …………………………………………………8分
…………………………………………………8分
(1) 假设存在实数,使 (
( )有最小值
)有最小值 ,
,
 ……………………………………………………9分
……………………………………………………9分
①
当 时,
时,
 ,
,

 在
在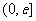 上单调递增,此时
上单调递增,此时 无最小值. …10分
无最小值. …10分
②当 时,
时,
若 ,故
,故 在
在 上单调递减,
上单调递减,
若 ,故
,故 在
在 上单调递增.
上单调递增.
 ,得
,得 ,满足条件. ……………………………12分
,满足条件. ……………………………12分
③当 时,
时,
 ,
,
 在
在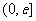 上单调递减,
上单调递减,
 (舍去),
(舍去),
所以,此时 无最小值. ……13分
无最小值. ……13分
综上,存在实数 ,使得当
,使得当 时
时 的最小值是
的最小值是 ……………………14分
……………………14分
(3)法二:假设存在实数,使
 的最小值是
的最小值是 ,
,
故原问题等价于:不等式 对
对 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.
即不等式 对
对 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.
设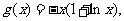 即
即 ,
, …………………………10分
…………………………10分
又 ……………………………………11分
……………………………………11分
令
当 ,
, ,则
,则 在
在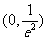 单调递增;
单调递增;
当 ,
, ,则
,则 在
在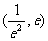 单调递减. ………………………………13分
单调递减. ………………………………13分
故当 时,
时, 取得最大值,其值是
取得最大值,其值是 .
.
故
综上,存在实数 ,使得当
,使得当 时
时 的最小值是
的最小值是 .……………………14分
.……………………14分
19. 解:(1)设
解:(1)设 ,由
,由 ,得
,得 ,……2分
,……2分
由 得
得 ,即
,即 ,
……5分
,
……5分
由于点P在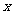 轴的正半轴上,所以
轴的正半轴上,所以 ,
,
故点M的轨迹C的方程为 (
( ) ……7分
) ……7分
(2)由 得
得 ,
……9分
,
……9分

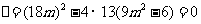 得
得 ,
, ,……10分
,……10分
因为 (
( )表示椭圆在
)表示椭圆在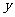 轴右边部分.
轴右边部分.
椭圆 的上顶点
的上顶点 ,
,
所以数形结合得
所以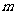 的取值范围为
的取值范围为 . ……14分
. ……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com