
22、设函数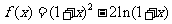 .
.
(Ⅰ)求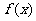 的单调区间;
的单调区间;
(Ⅱ)求函数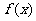 在
在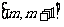
 上的最小值;
上的最小值;
(Ⅲ)若关于x的方程 在区间[0, 2]上恰好有两个相异的实根,求实数
在区间[0, 2]上恰好有两个相异的实根,求实数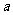 取值范围.
取值范围.
21、已知数列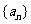 的前
的前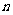 项和为
项和为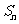 ,且对于任意的
,且对于任意的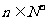 ,恒又
,恒又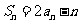 ,
,
(1)求证数列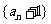 是等比数列;
是等比数列;
(2)设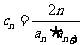 ,试判断数列
,试判断数列 的单调性,并求数列
的单调性,并求数列 的最大项。
的最大项。
19、有编号为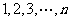 的
的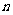 个学生,入坐编号为
个学生,入坐编号为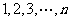 的
的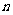 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为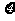 ,已知
,已知 时,共有
时,共有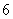 种坐法.
(Ⅰ)求
种坐法.
(Ⅰ)求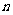 的值;
(Ⅱ)求随机变量
的值;
(Ⅱ)求随机变量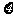 的概率分布列和数学期望.
的概率分布列和数学期望.

20如图,已知四棱锥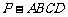 的底面是直角梯形,∠ABC
的底面是直角梯形,∠ABC ∠BCD
∠BCD 90°,AB
90°,AB BC
BC PB
PB PC
PC 2CD
2CD 2,侧面PBC⊥底面ABCD。
2,侧面PBC⊥底面ABCD。
(Ⅰ)求证: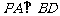 ;
;
(II)求二面角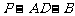 的余弦值。
的余弦值。
18、已知向量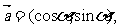
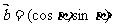 ,
,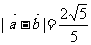 .
.
(1)求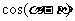 的值; (2)若0<
的值; (2)若0<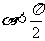 ,
, ,且
,且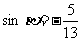 ,求
,求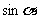 的值.
的值.
17、在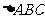 中,
中,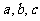 分别是角
分别是角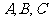 的对边,且
的对边,且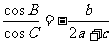 ,则角
,则角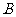 的大小为
的大小为
16、某校要求每位学生从7门课程中选修4门,其中甲乙两门课程不能都选,则不同的选课方案有___________种。
15、已知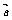 =(-1, 3),
=(-1, 3),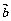 =(2, -1),若(k
=(2, -1),若(k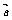 +
+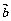 )⊥(
)⊥(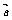 -2
-2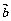 ),则k=
),则k=
14、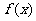 是定义在实数有R上的奇函数,若x≥0时,
是定义在实数有R上的奇函数,若x≥0时,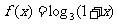 ,则
,则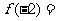 ______
______
13、若点P(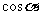 ,
,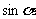 )在直线上
)在直线上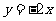 上,则
上,则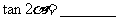
12、已知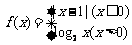 ,则
,则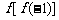 =_________.
=_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com