
2.第四段中,作者一连用了五个“为了”,在表达上有什么作用?
1.在首段中,作者说:“湖是大地的眼睛。”对这句话,你怎样理解?
4.第七段用一组简短的句子概括地写出了老王的心理和神态,假如你就是此时的老王,你的内心是怎样想的?
自然物语·借物抒情
湖
王 蒙
我喜爱湖。湖是大地的眼睛,湖是一种流动的深情。湖 是生活中没有被剥夺的一点奇妙。早在幼年时候,一见到北海公园的太液池,我就眼睛一亮。在贫穷和危险的旧社会,太液池是一个意外的惊喜,是一个奇异的温柔,一种孩提式的敞露与清流。
是生活中没有被剥夺的一点奇妙。早在幼年时候,一见到北海公园的太液池,我就眼睛一亮。在贫穷和危险的旧社会,太液池是一个意外的惊喜,是一个奇异的温柔,一种孩提式的敞露与清流。
我常常认为,大地与人之间有一种奇妙的契合。山是沉重的责任与名节的矜持。海是渺茫的遐思与变易的丰富。沙漠是希望与失望交织的庄严的等待。河流是一种寻求,一种机智,一种被辖制的自由……
那时候我没有见过海,颐和园的昆明湖对于我来说已经是浩浩然荡荡然的大水了。我每去一次颐和园,都要欣赏昆明湖的碧波,惊叹于湖水的美丽与自身的渺小。
是的,湖是一种美丽,是一种情意。为了陆地不那么干枯,为了人的生活不那么疲劳,为了把凶恶的海控制起来把生硬的地面活泼起来,为了你的眼睛与天上的月亮--你不觉得看到地面上的一个湖就像看到天上的月亮一样令人欣喜吗?为了短暂的焦渴的生命中不能或缺的滋润,于是有了湖。
北京的西山风景区是很美的,但是太缺少湖水了。这样,对于香山静宜园“双清”的池水,对于小小的儿童乐园式的眼镜湖,我自然是情有独钟。一见到这样的水波荡漾,脸上不由得出现衷心的笑容。
后来到了新疆以后,那就开了眼啦。在乌鲁木齐与伊梨之间的天山深处,著名的高山湖泊赛里木湖曾经怎么样地令人眼界开阔呀!湖水是咸的,湖水一 望无际,湛蓝如玉,盘山公路傍湖而过,无数拉运木材、粮食、水泥、钢筋、百货的重型卡车从湖边走过。四周是长满枞树的高处终年积雪的山坡。时而有强劲的风自由地吹过。我在这里,感觉到一种庄严,一种粗犷,一种阔大。我不能不庆幸我终于离开了大城市,离开了那一个区一个胡同一处房子。我面对着的是一个严峻的、带几分神秘和野性的世界。
望无际,湛蓝如玉,盘山公路傍湖而过,无数拉运木材、粮食、水泥、钢筋、百货的重型卡车从湖边走过。四周是长满枞树的高处终年积雪的山坡。时而有强劲的风自由地吹过。我在这里,感觉到一种庄严,一种粗犷,一种阔大。我不能不庆幸我终于离开了大城市,离开了那一个区一个胡同一处房子。我面对着的是一个严峻的、带几分神秘和野性的世界。 这个世界里有一个巨大而晶莹的
这个世界里有一个巨大而晶莹的 咸湖,它冷静而又尊严,凛然而又高耸地存在着。你觉得你其实只能向往它却很难有机会去亲近它。
咸湖,它冷静而又尊严,凛然而又高耸地存在着。你觉得你其实只能向往它却很难有机会去亲近它。
在天山南麓的焉耆与库尔勒之间,有一个大 湖--博斯腾湖,浩渺无际,芦苇丛生,坐着汽艇穿来穿去也见不到岸。据说有一个外国的总理看展览的时候看到博斯腾湖的照片甚感惊异,他说:“新疆不是不靠海吗?”那宛如内陆的海,那是远古时代的海的遗留,那是对于远离大海的新疆的特殊的慰安。
湖--博斯腾湖,浩渺无际,芦苇丛生,坐着汽艇穿来穿去也见不到岸。据说有一个外国的总理看展览的时候看到博斯腾湖的照片甚感惊异,他说:“新疆不是不靠海吗?”那宛如内陆的海,那是远古时代的海的遗留,那是对于远离大海的新疆的特殊的慰安。
在阿尔卑斯山的脚下,在芝加哥的北边,在布加勒斯特的市区,在高原墨西哥城近郊,我造访过许多湖泊。我流连忘返,我抱怨自己只能匆匆邂逅,匆匆离去,我太对不起上苍的得意创造与生活给予我的机缘。
而珠海斗门的白藤湖呢?它是1993年6月走入我的记忆的。这是又一种心绪,又一番风趣。它是那样亲切随意,那样为人所有为人所用。它是一种景观更是一种资源,它是一种大自然的慷慨,也是特有的风水--它象征着斗门人的、白藤湖人的无限发达的可能。度假村的修建已经开辟了新的历史。白藤湖是一个更加人化的湖,人化的自然。1993年我有幸在这里居住了若干天。居住在白藤湖,我觉得好舒适而又平安。我觉得发展其实并不难,生活其实也不是那么困难。只要好好地做,只要不把力量放在破坏上。只要我们变得更近人情一些,更简单一些。只要我们多一点美好的祝愿,少一点恶狠狠的狼眼。
(摘自《读写天地》2009年第5期)
回味无穷
在对湖的如数家珍中我们深深地感受到作者所流露出的喜爱之情,而这种情感来自于作者对湖的深刻的感悟。“我喜爱湖。湖是大地的眼睛,湖是一种流动的深情。湖是生活中没有被剥夺的一点奇妙。”作者开篇就奠定了全文的感情基调,接着我们与作者一起进行了一场游湖、品湖之旅。在描绘湖的时候,作者极尽细腻描写之能事,对湖展开了生动的描绘,令人陶醉其中,更重要的是作者饱含深情,从湖中品出难得的意蕴,抒发出真实的情感,给人无穷的回味。
且读且思
3.按照下面所提示的角度对句子进行简要赏析。
(1)如果一切都是调好了,印刷在DDD上,批量生产,效果同一,百分之百的把握,还有什么意思呀?(从语言风格上赏析)
(2)你经历了,你熟悉了,你重温着,你珍惜着,你温暖着也悲伤着……真好。(从句式角度进行赏析)
2.第二段作者不厌其烦地用“他听了……”的句式进行叙述,如果我们把这一段改成“老王听了无数好听的MP3”这样一句话,好不好?
1.老王那么喜欢听MP3,也非常喜欢搜歌的特别感觉,为什么到后来MP3笼不住老王的心了?
22.已知函数 .
.
(1)若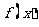 在
在 上是增函数,求实数的范围;
上是增函数,求实数的范围;
(2)设 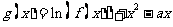 ,求证:
,求证: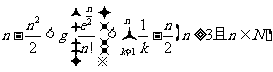 .
.
21.已知离心率为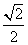 的椭圆
的椭圆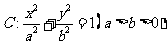 过点
过点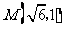 ,
,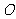 是坐标原点.
是坐标原点.
(1)求椭圆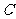 的方程;
的方程;
(2)已知点 为椭圆
为椭圆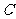 上相异两点,且
上相异两点,且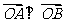 ,判定直线
,判定直线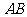 与圆
与圆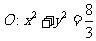 的位置关系,
的位置关系,
并证明你的结论.
20.设正项数列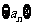 的前项和为
的前项和为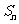 ,且
,且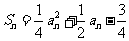 ,
,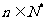 .
.
(1)求数列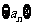 的通项公式;
的通项公式;
(2)是否存在等比数列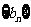 ,使
,使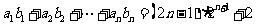 对一切正整数都成立?
对一切正整数都成立?
并证明你的结论.
19.如图,四棱锥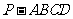 中,底面
中,底面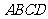 是平行四边形,
是平行四边形,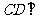 侧面
侧面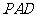 ,点在侧棱
,点在侧棱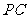 上,
上,
且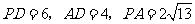 .
.
(1)求证:平面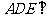 平面
平面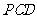 ;
;
 (2)若
(2)若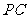 与
与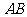 所成角为
所成角为 ,二面角
,二面角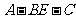 的大小为
的大小为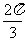 ,求
,求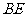 与平面
与平面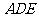 所成角的大小.
所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com