
5.1 插入法
将酯基插入烃的碳链中则为酯,此法也适用于醚和酮等。解法步骤:
第一步:先写去掉酯基余下组成(烃)的各可能的碳链结构;
第二步:将酯基以两种不同的方向(正向-COO-反向-OOC-分别插入第一步写出的各式的C-C键中;
第三步:将酯基以反向分别插入第一步写出的各式的C-H键中(若以正向插入则得羧酸)。
[例] 写出分子式为C5H10O2 且属于酯的的各种同分异构体的结构简式
 [解析] C4 只有两种碳链,将酯基按正反两种方向分别插入C-C键中,得5种酯(如下图所示);再将酯基按反向插入这两种碳架不同的C-H键中,则得到4种甲酸酯。因此 C5H10O2酯的异构体共有 9 种。
[解析] C4 只有两种碳链,将酯基按正反两种方向分别插入C-C键中,得5种酯(如下图所示);再将酯基按反向插入这两种碳架不同的C-H键中,则得到4种甲酸酯。因此 C5H10O2酯的异构体共有 9 种。
4.2 换元法
[例] 已知C6H4Cl2 有三种异构体,则C6H2Cl4有三种异构体。(将H代替Cl)

[练4-3] 已知A的结构为 A的n溴代物与m溴代物的异构体数目
相同,则n和m必满足关系式 m+n=6
5 酯的异构
4.1 有序法(定一移一)
有序法要求解决问题时遵循一定的特定线索和步骤去探索的一种思维方法。应用有序法解决烃的多元取代物异构体问题的步骤顺序是:先写出碳架异构,再在各碳架上依次先定一个官能团,接着在此基础上移动第二个官能团,依此类推,即定一移一。
[例] 二氯丙烷有 4 种异构体,它们的结构简式是

[解析]三个碳,碳链只有一种(不包括环)。先定一个氯原子在1号碳上,然后把第二个氯原子分别移到1、2、3 号碳上,得三种异构体;接着将一个氯定在2号碳上,此时第2个氯就只以能接在2号碳上,因此共得到4种异构体。解题中要注意判断排除重复的结构。
[练4-1] 苯丙醇胺(PPA)结构简式如下:

将-Ф、NH2、-OH在碳链上的位置作变换,还可以写出其它 8 种异构体(不包括-OH和-NH2连在同一碳原子的异构体。试写出包括PPA自身在内的这些异构体的结构简式。
[解析] 有序思维推导过程如下:
 第一步:先定位-Ф苯基,苯基在碳链上只有两种连接;
第一步:先定位-Ф苯基,苯基在碳链上只有两种连接;
 第二步:在定位了-Ф苯基所得到的二式中,分别变换-OH在碳链上的位置,得①-⑤
第二步:在定位了-Ф苯基所得到的二式中,分别变换-OH在碳链上的位置,得①-⑤
第三步:在定位了-Ф、-OH的上述①-⑤五个式中分别变换-NH2,共得到9种异构体。
 (注意按题意-NH2不能与-OH接在同一碳原子上 )
(注意按题意-NH2不能与-OH接在同一碳原子上 )
由①式得
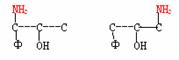
由②式得
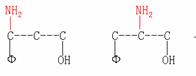
由③式得
 由④式得
由④式得

由⑤式得

[练4-2] 蒽的结构式为 它的一氯代物有 3 种,二氯代物有 15 种。
[解析] 蒽分子结构中有三种位置不同的氢,即有三种不同的等效氢,因此它的一氯取代产物有3种;二氯代物数推异的思路是:先写出三种一氯代物结构,再遂一分析各一氯代物又能衍生出几种二氯代物,要注意剔除重复的结构.
2.3 苯同系物的异构(侧链碳架异构及侧链位置的异构) 如C9H12有8种异构体:
3 烃的一元取代物的异构(取代等效氢法)
卤代烃、醇、醛、羧酸都可看着烃的一元取代物。确定它们异构体可用取代等效氢法。
等效氢概念
有机物分子中位置等同的氢叫等效氢,分子中等效氢原子有如下情况:
①分子中同一个碳原子上连接的氢原子等效。
②同一个碳原子上所连接的甲基上的氢原子等效。如新戊烷(可以看作四个甲基取代了甲烷分子中的四个氢原子而得),其四个甲基等效,各甲基上的氢原子完全等效,也就是说新戊烷分子中的12个H原子是等效的。
③分子中处于镜面对称位置(相当于平面镜成像时,物与像的关系)上的氢原子是等效的。如 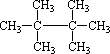 分子中的18个H原子是等效的。
分子中的18个H原子是等效的。
取代等效氢法要领
利用等效氢原子关系,可以很容易判断出有机物的一元取代物异构体数目。其方法是先写出烃(碳架)
的异构体,观察分子中互不等效的氢原子有多少种,则一元取代物的结构就有多少种。
 C3H7X 一种碳链,共有 2 种异构体
C4H9X 二种碳链,共有 4 种异构体
C3H7X 一种碳链,共有 2 种异构体
C4H9X 二种碳链,共有 4 种异构体

 C5H11X
3种碳链,共有 8 种异构体
C5H11X
3种碳链,共有 8 种异构体
这里的一元取代基X,可以是原子,如卤原子,也可以是原子团,如-OH、-CHO、-COOH、HCOO-等。因此,已知丁基-C4H9有四种,则可断定丁醇、戊醛、戊酸以及甲酸丁酯都有4种异构体。
观察并找出分子结构中的对称要素是取代等效氢法的关键
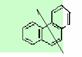
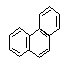 例:菲和蒽互为同分异构体,菲的结构简式为 从菲的结构简式分析,菲的一氯取代物共有(B)
例:菲和蒽互为同分异构体,菲的结构简式为 从菲的结构简式分析,菲的一氯取代物共有(B)
A.4种 B.5种 C.10种 D.14种
提示:找出菲结构的对称轴,则答案显见。
[练3-1] 分子式为C11H16的一烷基取代苯的同分异体共有 8 种
[解析] 一烷基取代苯[C6H5-C5H11]可看作苯基取代戊烷中的一个氢,而戊基有8种异构体,所以C11H16共有8 种一烷基取代苯的同分异构体。
[练3-2]蓝烷分子结构如 ,试写出蓝烷分子式:C10H10,它的一氯代物共有 4 种。
,试写出蓝烷分子式:C10H10,它的一氯代物共有 4 种。
{说明}常可根据某些烃存在的一元取代物数目,反推原烃分子结构式。如含碳原数少于10的烷烃中,其中一卤代物不存在异构体的有 4 种。
又如,已知烯烃C6H12的一氯代物只有一种,则可断定该烯烃的分子结构为

4 烃的二元(或三元)取代物的异构
2.2 烯炔的异构(碳架的异构和碳碳双键或叁键官能团的位置异构)

如丁烯C4H8有两种碳链,形成3种异构体:
1 概念辩析(同分异构、同一种物质、同系物)
同分异构:化合物具有相同的分子式,但结构不同的现象称为同分异构现象。具有同分异构现象的化合物互称为同分异构体。在中学阶段,引起同分异构的原因主要有三种:碳架异构、位置异构和官能团异构。识别两者是否是同分异构体,首先要查碳原子数,判别分子式是否相同,然后再看结构式。在分子式相同的情况下,若结构不同,则两者必为同分异构体。
同一种物质:两者不仅分子式相同,而且结构也完全相同,则为同一种物质。同一种物质应具有相同的物理参数,如有相同的熔沸点。判断两结构是否相同方法有二:(1)将分子整体翻转或沿对称要素(面、线)旋转后能“重合”者;(2)用系统命名法命名,所得名称相同者。
同系物:结构相似,在分子组成上相差一个或几个CH2原子团的物质互称同系物。结构相似是指分子中含有官能团的种类和数目都要相同。如乙醇与丙醇为同系物,但乙二醇与丙三醇就不属同系物了。
若已知两结构式要判断它们是否具有相同的分子式,数不饱和度要比数氢原子数目快捷得多。在C、O、N、Cl等原子数对应相同的前提下,不饱和度相同的,分子式一定相同。 如:
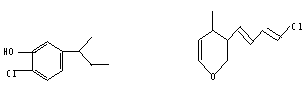
两者C、O、Cl原子数相同,不饱度都是4,所以两结构式具有相同的分子式。而结构显然不同,因此两者应为同分异构体。
对于稠环芳香烃利用公用边数目来确定两个已知结构式的关系则很方便。在苯环数相同的前提下,若公用边数相同,且各苯环排列顺序又相同,则两者表示的是同一种物质;若公用边数相同,且各苯环排列顺序不相同,则两者表示的是同分异构体;若公用边数不同,则两者即不是同分异构体,也不是同一物物质。
 [练1-1]下列4式表示的是棉子象鼻虫的四种的信息素的结构简式,其中互为同分异构体是(③④)
[练1-1]下列4式表示的是棉子象鼻虫的四种的信息素的结构简式,其中互为同分异构体是(③④)
解析:②中含10个碳原子,①③④都有11个碳原子,③含一个-CH2OH,比①式(含一个-CHO)多二个氢,故①③不是同分异构体。③④分子式相同,但③式是一个六元环,④式是一个四元环,两者结构不同,故互为同分异构体。
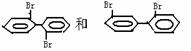
[练1-2] 下列各组物质中属于同分异构体的是⑴⑶,属于同系物的是⑵,既不是同系物又不同分异构体的是⑷,属于同一种物质的是⑸。
 ①
⑤
①
⑤
②乙酸和硬脂酸 ③硝酸乙烷和氨基乙酸 ④苯甲酸和对苯二甲酸
解析: ①组属于同分异构体,分子式都是C7H8O,但前者属芳香醇,后者属酚;②组属同系物,同属一元脂肪酸系列,分子组成相差16个CH2;③是同分异构体,要掌握同碳数的硝基烷和氨基酸是互为类别异构;④组两者含碳数不同,不是同分异构体,两者虽都有含羧基-COOH,但含有羧基数不同,也不属同系物。⑤组要注意到C-C单键可绕键轴旋转,故两结构式是相同,表示的是同一种物质。
[练1-3] 萘分子的结构可以表示为  或
或  ,两者是等同的。苯并[α]芘是强致癌物质(存在于烟囱灰、煤焦油、燃烧的烟雾和内燃机的尾气中)。它的分子由5个苯环并合而成,其结构式可以表示为(Ⅰ)或(Ⅱ)式:
,两者是等同的。苯并[α]芘是强致癌物质(存在于烟囱灰、煤焦油、燃烧的烟雾和内燃机的尾气中)。它的分子由5个苯环并合而成,其结构式可以表示为(Ⅰ)或(Ⅱ)式:





 (Ⅰ)
(Ⅰ) (Ⅱ)
(Ⅱ)
这两者也是等同的。现有结构式A、B、C、D:

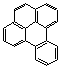


A B C D
其中:与(Ⅰ)、(Ⅱ)式等同的结构式是( );
与(Ⅰ)、(Ⅱ)式同分异构体的是( )。
[解析] 以(Ⅰ)式为基准,图形从纸面上取出向右翻转180°后再贴回纸面即得D式,将D式在纸面上逆时针旋转45°即得A式。因此,A、D都与(Ⅰ)、(Ⅱ)式等同。也可以(Ⅱ)式为基准,将(Ⅱ)式图形在纸面上反时针旋转180°即得A式,(Ⅱ)式在纸面上逆时针旋转135°即得D式。
从分子组成来看,(Ⅰ)式是C20H12,B式也是C20H12,而C式是C19H12,所以B是Ⅰ、Ⅱ 的同分异构体,而C式不是。
稠环芳烃共用边数法 A与D 两式共用边都是 6条,且五个苯环的排列顺序实质是一样的,所以两式表示的是同一种物质。A 与 B(或D与B )五个苯环都共用6条边,但苯环的排列顺序不一样,所以它们互为同分异构体。而C式五个苯环共用的是7条边,因此 C 与其它三式即不是同分异构体,也不是同一种物质。
答案是(1)AD;(2)B。
2 烃的异构
2.1 烷烃的异构(碳架的异构)
熟记C1-C6的碳链异构: CH4、C2H6、C3H8 无异构体;C4H10 2种、C5H12 3种、C6H14 5种。
2、同系物的判断规律
(1)一差(分子组成差一个或若干个CH2);
(2)二同(同通式,同结构);
(3)三注意:①必为同一类物质
②结构相似(有相似的原子连接方式或相同的官能团种类和数目)
③同系物间物理性质不同,化学性质相似,因此,具有相同通式的有机物除烷烃外都不能确定是不是同系物。
1、定义:
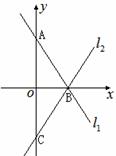
25.已知,如图,直线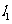 :
: 与
与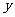 轴交于点
轴交于点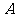 ,与直线
,与直线 交于
交于 轴上同一点
轴上同一点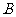 ,直线
,直线 交
交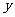 轴于点
轴于点 ,且点
,且点 与点
与点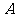 关于
关于 轴对称.
轴对称.
(1)求直线 的解析式.
的解析式.
(2)若点 是直线
是直线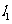 上任意一点,求证:点
上任意一点,求证:点 关于
关于 轴的对称点
轴的对称点 一定在直线
一定在直线 上.
上.
(3)设 ,平行于
,平行于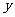 轴的直线
轴的直线 分别交直线
分别交直线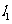 和
和 于点
于点 、
、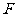 . 是否存在
. 是否存在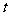 的值,使得以
的值,使得以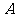 、
、 、
、 、
、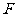 为顶点的四边形是平行四边形,若存在,求出
为顶点的四边形是平行四边形,若存在,求出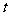 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
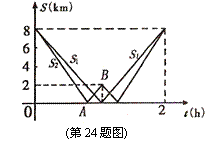
24、(本小题满分10分)在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),下图中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km;
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com