
21、(本题满分16分)已知定点A(0,1),B(0,-1),C(1,0)。动点P满足: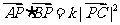 。
。
(1)求动点P的轨迹方程,并说明方程表示的曲线;(2)当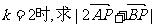 的最大值和最小值。
的最大值和最小值。
解:(1)设动点的坐标为P(x,y),则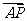 =(x,y-1),
=(x,y-1),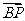 =(x,y+1),
=(x,y+1),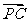 =(1-x,-y)
=(1-x,-y)
∵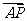 ·
·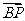 =k|
=k|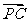 |2,∴x2+y2-1=k[(x-1)2+y2] 即(1-k)x2+(1-k)y2+2kx-k-1=0。
|2,∴x2+y2-1=k[(x-1)2+y2] 即(1-k)x2+(1-k)y2+2kx-k-1=0。
若k=1,则方程为x=1,表示过点(1,0)是平行于y轴的直线。
若k≠1,则方程化为: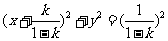 ,
,
表示以(-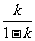 ,0)为圆心,以
,0)为圆心,以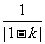 为半径的圆。
为半径的圆。
(2)当k=2时,方程化为(x-2)2+y2=1。∵2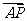 +
+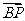 =2(x,y-1)+(x,y+1)=(3x,3y-1),
=2(x,y-1)+(x,y+1)=(3x,3y-1),
∴|2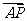 +
+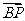 |=
|=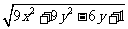 。又x2+y2=4x-3,
。又x2+y2=4x-3,
∴|2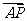 +
+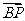 |=
|= ∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。
∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。
则36x-6y-26=36cosθ-6sinθ+46=6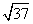 cos(θ+φ)+46∈[46-6
cos(θ+φ)+46∈[46-6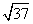 ,46+6
,46+6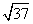 ],
],
∴|2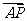 +
+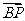 |max=
|max=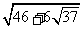 =3+
=3+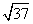 ,|2
,|2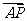 +
+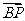 |min=
|min=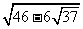 =
=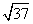 -3。
-3。
20、(本题满分14分)已知双曲线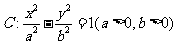 的两个焦点为
的两个焦点为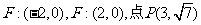 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为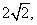 求直线l的方程
求直线l的方程
(Ⅰ)解:依题意,由a2+b2=4,得双曲线方程为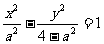 (0<a2<4
(0<a2<4 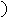
将点(3,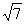 )代入上式,得
)代入上式,得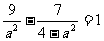 .解得a2=18(舍去)或a2=2,
.解得a2=18(舍去)或a2=2,
故所求双曲线方程为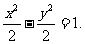
(Ⅱ)解:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.
∵直线I与双曲线C相交于不同的两点E、F,
∴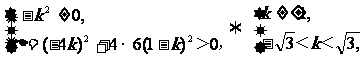
∴k∈(-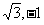 )∪(1,
)∪(1,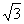 ).
).
设E(x1,y1),F(x2,y2),则由①式得x1+x2=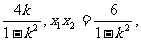 于是
于是
|EF|=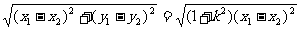
=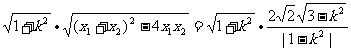
而原点O到直线l的距离d=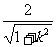 ,
,
∴SΔOEF=
若SΔOEF=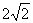 ,即
,即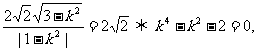 解得k=±
解得k=±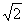 ,
,
满足②.故满足条件的直线l有两条,其方程分别为y=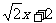 和
和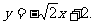
19、(本题满分14分)圆的方程为x2+y2-6x-8y=0,过坐标原点作长为8的弦,求弦所在的直线方程。
解:x2+y2-6x-8y=0即(x-3)2+(y-4)2=25,设所求直线为y=kx。
∵圆半径为5,圆心M(3,4)到该直线距离为3, ∴ 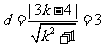 ,
,
∴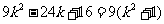 ,∴
,∴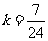 。 ∴所求直线为y
。 ∴所求直线为y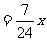 或
或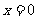 。
。
18、在圆x2+y2=5x内,过点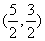 有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差
有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差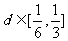 ,那么n的取值集合为( A
)
,那么n的取值集合为( A
)
A.{4,5,6,7} B.{4,5,6} C.{3,4,5,6} D. {3,4,5}
17、抛物线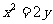 离点A(0,a)最近的点恰好是顶点,这个结论成立的充要条件是( C)
离点A(0,a)最近的点恰好是顶点,这个结论成立的充要条件是( C)
A.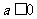 B.
B. 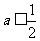 C.
C.
 D.
D.
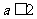
16、过双曲线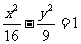 左焦点F1的弦AB长为6,则
左焦点F1的弦AB长为6,则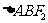 (F2为右焦点)的周长(A)
(F2为右焦点)的周长(A)
A.28 B.22 C.14 D.12
15、直线l经过A(2,1)、B(1,m2)(m∈R)两点,那么直线l的倾斜角的取值范围是( D )
A.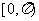 B.
B.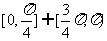 C.
C.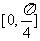 D.
D.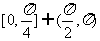
14、已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
1) 对任意实数k与q,直线l和圆M相切;
2) 对任意实数k与q,直线l和圆M有公共点;
3) 对任意实数q,必存在实数k,使得直线l与和圆M相切
(4)对任意实数k,必存在实数q,使得直线l与和圆M相切
其中真命题的代号是____________(2)(4) (写出所有真命题的代号)
13、已知AB是椭圆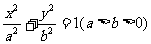 的长轴,若把该长轴
的长轴,若把该长轴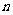 等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点
等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点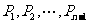 ,设左焦点为
,设左焦点为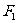 ,则
,则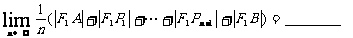
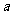
12、已知两点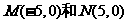 ,若直线上存在点
,若直线上存在点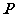 ,使
,使 ,则称该直线为“
,则称该直线为“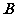 型直线”.给出下列直线:①
型直线”.给出下列直线:①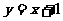 ;②
;②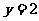 ;③
;③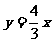 ;④
;④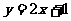 ,其中为“
,其中为“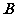 型直线”的是___________①②
型直线”的是___________①②
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com