
29. The day we had been looking forward to _____ at last.
|
|
A. come |
B. came |
C. coming |
D. be
coming |
28. We had an anxious couple of weeks _____ for the results of the experiment.
|
|
A. wait |
B. to be
waiting |
C. waited |
D. waiting |
27. I hear they’ve promoted Tom, but he didn’t mention _____ when we talked on the phone.
|
|
A. to
promote |
B. having
been promoted |
|
|
C. having
promoted |
D. to be
promoted |
26. We went right round to the west coast by _____ sea instead of driving across _____ continent.
|
|
A. the; the
|
B. /; the |
C. the; / |
D. /; / |
Section A
Directions: Beneath each of the following sentences there are four choices marked A, B, C and D. Choose the one answer that best completes the sentence.
25. I called Alice many times yesterday evening, but I couldn’t get through. Her brother _____ on the phone all the time!
|
|
A. was
talking |
B. has been
talking |
C. has
talked |
D. talked |
Section A
Directions: In Section A; you will hear ten short conversations between two speakers. At the end of each conversation, a question will be asked about what was said. The conversations and the questions will be spoken only once. After you hear a conversation and the question about it, read the four possible answers on your paper, and decide which one is the best answer to the question you have heard.
|
1. |
A. In a
hotel. |
B. At a
dinner table. |
C. In the
street. |
D. At the
man’s house. |
|
2. |
A. France. |
B. Britain. |
C. Germany. |
D. Spain. |
|
3. |
A. A
writer. |
B. A teacher. |
C. A
reporter. |
D. A
student. |
|
4. |
A.
Librarian and students. |
B. Operator
and caller. |
||
|
|
C. Boss and
secretary. |
D. Customer
and repairman. |
||
|
5. |
A. Five
lessons. |
B. Three
lessons. |
C. Twelve
lessons. |
D. Fifteen
lessons. |
|
6. |
A. The man
is planning a trip to Austin. |
B. The man
has not been to Austin
before. |
||
|
|
C. The man doesn’t
like Austin. |
D. The man
has been to Austin
before. |
||
|
7. |
A. Find a
larger room. |
B. Sell the
old table. |
||
|
|
C. Buy two
bookshelves. |
D.
Rearrange some furniture. |
||
|
8. |
A. The
choice of courses. |
B. A day
course. |
||
|
|
C. An
evening course. |
D. Their
work. |
||
|
9. |
A. It was a
long lecture, but easy to understand. |
|||
|
|
B. It was
not as easy as she had expected. |
|||
|
|
C. It was
as difficult as she had expected. |
|||
|
|
D. It was
interesting and easy to follow. |
|||
|
10. |
A. She felt
it was tiring. |
B. She felt
it was very nice. |
||
|
|
C. She felt
it took less time. |
D. She
thought it was expensive. |
Section B
Directions: In Section B, you will hear two short passages, and you will be asked to questions on each of the passages. The passages will be read twice, but the questions will spoken only once. When you hear a question, read the four possible answers on your paper decide which one would be the blest answer to the question you have heard.
Questions 11 through 13 are based on the following passage.
|
11. |
A.
Synthetic fuel. |
B. Solar
energy. |
C. Alcohol.
|
D.
Electricity. |
|
12. |
A. Air traffic
conditions. |
B. Traffic
jams on highways. |
||
|
|
C. Road conditions. |
D. New
traffic rules. |
||
|
13. |
A. Go
through a health check. |
B. Take
little luggage with them. |
||
|
|
C. Arrive
early for boarding. |
D. Undergo(进行) security checks. |
Questions 14 through 16 are based on the following news.
|
14. |
A.
Industry. |
B.
Agriculture. |
C. Public
health. |
D.
Environment. |
|
15. |
A. Three
thousand million dollars. |
B. Three
hundred million dollars. |
||
|
|
C.
Thirty-two thousand million dollars. |
D.
Twenty-three thousand million dollars. |
||
|
16. |
A.
Production problems. |
|||
|
|
B. Failure
to use the right chemicals. |
|||
|
|
C. the
active chemicals are stronger than permitted by government. |
|||
|
|
D. Both A
and B. |
Section C
Directions: In Section C, you will hear two longer conversations. The conversations will be read twice. After you hear each conversation, you are required to fill in the numbered blanks with the information you have heard. Write your answers on your answer sheet.
Blanks 17 through 20 are based on the following conversation.
|
Telephone message From: Tom, Prof. Smith’s student. To: Prof. Smith. Message: tom’s class is working on an English __17__. And they would like you to give them some __18__. Call him back at __19__ before __20__. |
Complete the form. Write ONE WORD for each answer.
Blanks 21 through 24 are based on the following conversation.
|
Plan for Vacation |
||
|
Ann |
Mike |
|
|
Place |
Would like
to go to the (21)____________. |
Thinking of
spending one week (23)_______________ and the remaining week visiting London. |
|
Reasons |
Likes
sports and (22)_____________ activities. |
a. A lot of work to be done. b. A revisit to their (24)_____________ place. |
Complete the form. Write NO MORE THAN THREE WORDS for each answer.
5.求点到面的距离一般有三种办法:①直接法---过“点”
作“面”的垂线(尽可能找到过这一点的一个与“面”垂直的
平面,然后过“点”作它们交线的垂线);②等积转换;③法向量: 若平面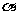 的法向量为
的法向量为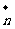 ,直线AB与平面
,直线AB与平面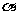 交于点A,则点B到平面
交于点A,则点B到平面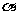 的距离
的距离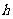 =
=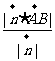 。
。
[举例1] 已知线段AD∥平面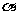 ,且与平面
,且与平面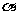 的距离为4,点B是平面
的距离为4,点B是平面 内的动点,且满足AB=5,AD=10,则B、D两点之间的距离
( )
内的动点,且满足AB=5,AD=10,则B、D两点之间的距离
( )
A.有最大值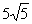 ,无最小值; B.有最小值
,无最小值; B.有最小值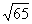 ,无最大值;
,无最大值;
C.有最大值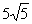 ,最小值
,最小值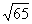 ; D.有最大值
; D.有最大值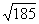 ,最小值
,最小值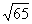 ;
;
解析:记A、D在面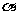 内的射影分别为A1、D1,∵AB=5,AA1=4,∴A1B=3,即B在面
内的射影分别为A1、D1,∵AB=5,AA1=4,∴A1B=3,即B在面 内以A1为圆心、3为半径的圆周上,又A1D1=10,故D1B最大为13,最小为7,而DD1=4,于是:由勾股定理得BD最大
内以A1为圆心、3为半径的圆周上,又A1D1=10,故D1B最大为13,最小为7,而DD1=4,于是:由勾股定理得BD最大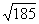 ,最小
,最小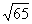 ,选D。
,选D。
|
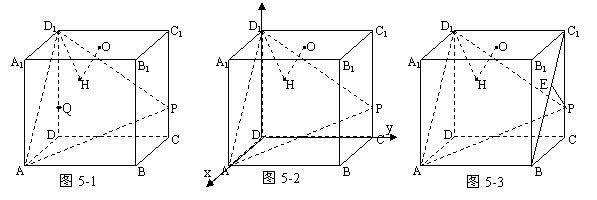
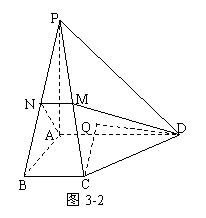
解析:方法一:“等积转换”。如果直接研究三棱锥P-ABD1的体积,无论怎样“转换”都不易求;在DD1上取一点Q,使DD1=4DQ,则PQ∥面ABD1,如图5-1;故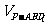 =
=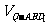 ,
,
记P到面ABD1的距离为h,则Q到面ABD1的距离为h, 由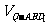 =
=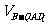 得:h=
得:h=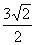 ;
;
方法二:以D为原点建系,如图5-2,A(4,0,0),B(4,4,0),D1(0,0,4),
P(0,4,1),不难求出面ABD1的法向量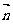 =(1,0,1),
=(1,0,1),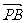 =(4,0,-1), h=
=(4,0,-1), h=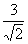 =
=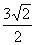 ;
;
方法3:“补齐”截面ABD1即正方体的对角面ABC1D1,过P作PE⊥BC1于E,如图5-3,
∵PE⊥AB,∴PE⊥面ABD1,∴PE的长度即为点P到平面ABD1的距离,易求PE=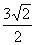 。
。
[巩固1]已知平面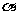 ∥平面
∥平面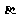 ,直线
,直线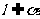 ,点
,点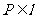 ,平面
,平面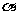 、
、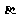 之间的距离为8,则在
之间的距离为8,则在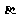 内到P点的距离为9的点的轨迹是:
( )
内到P点的距离为9的点的轨迹是:
( )
A.一个圆 B.两条直线 C.四个点 D.两个点
[巩固2](1)
正三棱锥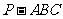 的高为
的高为 ,侧棱与底面
,侧棱与底面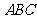 成
成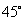 角,则点
角,则点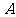 到侧面
到侧面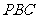 的距离为_____(07高考江苏卷14)。(2)正三棱柱
的距离为_____(07高考江苏卷14)。(2)正三棱柱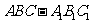 的所有棱长都为
的所有棱长都为 ,
,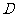 为
为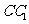 中点,则点
中点,则点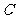 到平面
到平面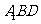 的距离为 (07高考福建理18).
的距离为 (07高考福建理18).
4.求二面角的方法很多,概括起来有两类,一类是作平面角,一类是不作平面角。作平面角又有直接作和间接作两种,形形色色的方法都是在做一件事:作二面角的棱的垂面;而不作平面角,要么建系用法向量求,要么用公式cos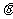 =
=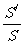 (其中S表示平面
(其中S表示平面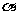 内的封闭图形C的面积,S/表示C在平面
内的封闭图形C的面积,S/表示C在平面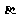 内的射影C/的面积,
内的射影C/的面积,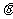 表示
表示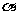 与
与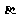 所成的锐二面角的大小)。二面角
所成的锐二面角的大小)。二面角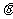 的范围(00,1800)。如cos
的范围(00,1800)。如cos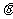 =-
=-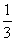 ,则
,则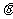 = arccos(-
= arccos(-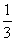 )=
)=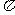 - arccos
- arccos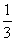 。
。
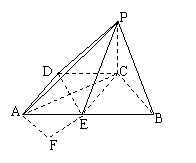
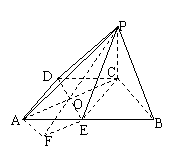 [举例]如图在四棱锥P-ABCD中,底面ABCD是
[举例]如图在四棱锥P-ABCD中,底面ABCD是
直角梯形,∠ADC=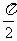 ,AB∥CD,PC⊥面ABCD,
,AB∥CD,PC⊥面ABCD,
PC=AD=DC=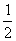 AB,E为线段AB的中点。
AB,E为线段AB的中点。
(1)求证:平面PAC⊥平面PDE;
(2)求二面角A-PE-D的大小。
解析:(1)在直角梯形ABCD中,容易知道四边形AECF是
正方形,∴DE⊥AC,又DE⊥PC∴DE⊥面PAC,∴面PDE⊥面PAC;(2)记PC=a,
 方法一:用三垂线定理作二面角的平面角。记AC、DE交于O,连PO,PO是相互垂直的平面PDE和PAC的交线,过A作PO的垂线交PO(的延长线)于F,则AF⊥面PDE,即F是A在面PDE内的射影,又容易证明AE⊥面PEC,则AE⊥PE,于是FE⊥PE,∴∠AEF是二面角A-PE-D的平面角;在⊿PAO中有面积相等不难算出AF=
方法一:用三垂线定理作二面角的平面角。记AC、DE交于O,连PO,PO是相互垂直的平面PDE和PAC的交线,过A作PO的垂线交PO(的延长线)于F,则AF⊥面PDE,即F是A在面PDE内的射影,又容易证明AE⊥面PEC,则AE⊥PE,于是FE⊥PE,∴∠AEF是二面角A-PE-D的平面角;在⊿PAO中有面积相等不难算出AF=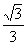 a,而AE=a,在Rt⊿AFE中,∠AEF=arcsin
a,而AE=a,在Rt⊿AFE中,∠AEF=arcsin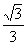 。注:用三垂线定理作二面角的平面角,是作二面角的平面角的最常用、最重要的方法。其过程概括为:找一垂--找(作)一个面内一点P在另一个面内的射影P/,作二垂--过P(或P/)作二面角棱l的垂线,垂足为Q,连三垂--连P/Q,则l⊥P/Q,于是∠PQ P/为二面角的平面角;计算该角在直角三角形内进行;在上述过程中,“找一垂”是关键。方法二:射影“悬空”作二面角的平面角
。注:用三垂线定理作二面角的平面角,是作二面角的平面角的最常用、最重要的方法。其过程概括为:找一垂--找(作)一个面内一点P在另一个面内的射影P/,作二垂--过P(或P/)作二面角棱l的垂线,垂足为Q,连三垂--连P/Q,则l⊥P/Q,于是∠PQ P/为二面角的平面角;计算该角在直角三角形内进行;在上述过程中,“找一垂”是关键。方法二:射影“悬空”作二面角的平面角
注意到AE⊥PE,记点A在面PDE内的射影为F
(无须知道点F的确切位置),连EF,则PE⊥FE,于是
∠AEF是二面角A-PE-D的平面角;以下问题化归
到求AF的长度(即A点到面PDE的距离)上。以下
用“等积转换”求AF,计算略。
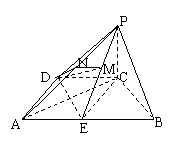 方法三:利用平面图形的有关性质作二面角的平面角
方法三:利用平面图形的有关性质作二面角的平面角
注意到DP=DE=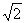 a,取PE的中点M,则PE⊥DM,
a,取PE的中点M,则PE⊥DM,
又容易知道AE⊥PE,取PA的中点N,连NM,则
NM∥AE,∴PE⊥MN,于是∠NMD为二面角A-PE-D
的平面角;以下在⊿DMN中,用余弦定理求∠NMD,
计算略。
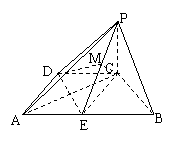 方法四:用割补法求。视二面角A-PE-D为二面角A-PE-C
方法四:用割补法求。视二面角A-PE-D为二面角A-PE-C
与二面角D-PE-C的差。对二面角A-PE-C,
∵ AE⊥面PEC,∴面AEP⊥面PEC,
即二面角A-PE-C为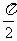 ;对二面角D-PE-C,点C是点D
;对二面角D-PE-C,点C是点D
在面PEC内的射影,取BE的中点M,∵CP=CE=a,
∴PE⊥MC,于是有:PE⊥MD,则∠DMC为二面角D-PE-C的平面角,
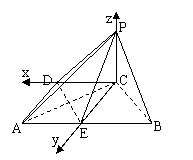 在Rt⊿DCM中,∠DMC=arctan
在Rt⊿DCM中,∠DMC=arctan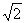 ,∴二面角A-PE-D的大小为
,∴二面角A-PE-D的大小为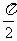 - arctan
- arctan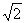 。
。
注:在求钝二面角时“割补法”往往很有效。
方法五:用平面的“法向量”求
∵CP⊥CE, CP⊥CD, CE⊥CD,故可以C为原点,
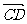 、
、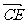 、
、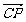 分别为x、y、z轴建立空间
分别为x、y、z轴建立空间
直角坐标系。A(a,a,0)、D(a,0,0)、E(0,a,0)、
P(0,0,a),则 =(a,0,0),
=(a,0,0),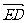 =(a,-a,0),
=(a,-a,0),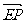 =(0,-a,a)
=(0,-a,a)
由此不难求出平面PAE的法向量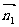 =(0,1,1), 平面PAE的法向量
=(0,1,1), 平面PAE的法向量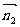 =(1,1,1)
=(1,1,1)
 则有:cos<
则有:cos<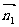 ,
,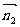 >=
>=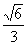 ,∴二面角A-PE-D的大小为arccos
,∴二面角A-PE-D的大小为arccos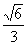 。注:用“法向量”求二面角有一处严重的不足:二面角两个面的法向量的夹角
。注:用“法向量”求二面角有一处严重的不足:二面角两个面的法向量的夹角
未必等于二面角,也可能与二面角互补,这取决于法向量
的方向,而确定法向量的方向却是中学生力不能及的。
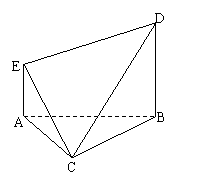
[巩固] 如图,在多面体ABCDE中,AE⊥面ABC,
BD∥AE,且AC=AB=BC=BD=2,AE=1,求面CDE与
面CAB所成的锐二面角.
3. 直线与平面所成的角要“抓住”直线在平面内的射影,然后在直角三角形内求得;直线与平面所成的角是直线与平面内任意直线所成角的最小值。线面角的范围:[00,900]。
直线与平面所成的角要“抓住”直线在平面内的射影,然后在直角三角形内求得;直线与平面所成的角是直线与平面内任意直线所成角的最小值。线面角的范围:[00,900]。
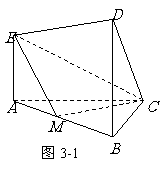
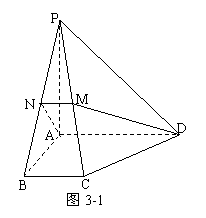
[举例1] 在如图3-1所示的几何体中, 平面
平面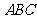 ,
,
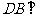 平面
平面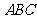 ,
,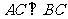 ,且
,且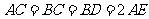 ,
,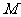 是
是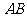 的中点.求
的中点.求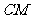 与平面
与平面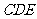 所成的角.
所成的角.
(07高考浙江理16)
解析:方法一:“找射影”。过M作MF⊥ED于F,连CF,
由CM⊥AB,CM⊥AE得CM⊥面ABDE,故CM⊥ED,
∴ED⊥面CMF,于是有面CED⊥面CMF于CF,过M作MH⊥CF
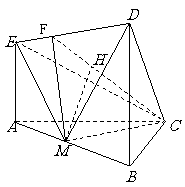 于H,则MH⊥面CED,∴∠MCH为
于H,则MH⊥面CED,∴∠MCH为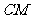 与平面
与平面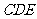 所成的角;
所成的角;
设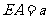 ,
,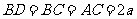 ,
,
在直角梯形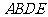 中,
中,
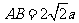 ,
,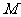 是
是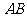 的中点,
的中点,
所以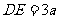 ,
,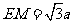 ,
,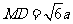 ,
,
得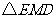 是直角三角形,其中
是直角三角形,其中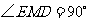 ,∴MF=
,∴MF=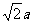
在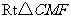 中,CM=MF,∴
中,CM=MF,∴ 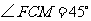 ,故
,故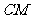 与平面
与平面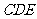 所成的角是
所成的角是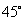 .
.
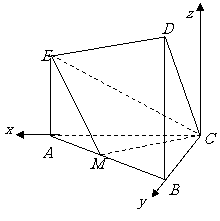 注:“作垂面”是求作点M在面
注:“作垂面”是求作点M在面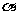 内的射影的最重要、最常用的方法,其过程是:过M点作平面
内的射影的最重要、最常用的方法,其过程是:过M点作平面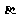 ⊥
⊥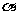 于
于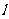 ,则M在面
,则M在面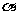 内的射影M/∈
内的射影M/∈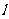 。
。
方法二:“建系”。如图,以点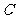 为坐标原点,以
为坐标原点,以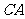 ,
,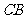
分别为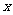 轴和
轴和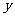 轴,过点
轴,过点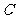 作与平面
作与平面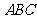 垂直的直线为
垂直的直线为
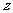 轴,建立直角坐标系
轴,建立直角坐标系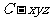 ,设
,设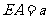 ,则
,则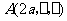 ,
,
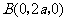 ,
,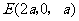 .
.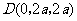 ,
,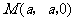 .
.
设向量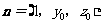 与平面
与平面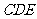 垂直,
垂直,
则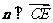 ,
,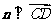 ,即n·
,即n·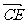 =0 , n·
=0 , n·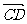 =0,∵
=0,∵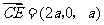 ,
,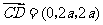 ,
,
得: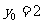 ,
,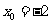 ,即
,即 ,由向量夹角公式得:cos< n,
,由向量夹角公式得:cos< n,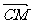 >=
>=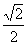 ,
,
直线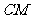 与平面
与平面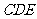 所成的角
所成的角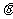 是
是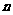 与
与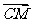 夹角的余角,所以
夹角的余角,所以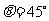 ,
,
故直线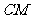 与平面
与平面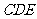 所成的角是
所成的角是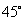 .
.
注:线与面的法向量所成的角与线面角互余;注意到线面角不为钝角,故:AB与面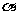 所成的角为:arcsin
所成的角为:arcsin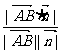 (
(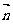 为面
为面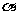 的法向量)。用法向量求线面角,以计算代替说理(找射影),最大限度地实现了“去逻辑化”,为疏于逻辑思维的同学求线面角提供了一条相对方便的路径;但是,并非所有的空间形体都可以建立适当的坐标系。
的法向量)。用法向量求线面角,以计算代替说理(找射影),最大限度地实现了“去逻辑化”,为疏于逻辑思维的同学求线面角提供了一条相对方便的路径;但是,并非所有的空间形体都可以建立适当的坐标系。
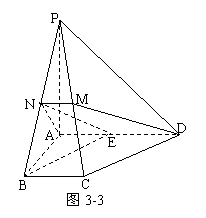
 [举例2]如图3-1,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点. 求CD与平面ADMN所成的角。
[举例2]如图3-1,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点. 求CD与平面ADMN所成的角。
解析:确定C点在面ADMN上的射影Q的位置很困难。方法一:“射影悬空”。先不管Q点的位置,∠CDQ为CD与平面ADMN所成的角,入图3-2;记BC=a,在Rt⊿CQD中,CD=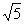 a,只需求出CQ(C到面ADMN的距离)即可,记为h;注意到
a,只需求出CQ(C到面ADMN的距离)即可,记为h;注意到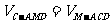 ,不难知道
,不难知道
⊿AMD中AD边上的高为AN,AN=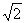 a,∴
a,∴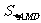 =
=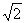 a2;
a2;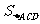 =2a2,M到面ACD的距离为a,
=2a2,M到面ACD的距离为a,
∴h=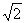 a,故在Rt⊿CQD中,∠CDQ= arcsin
a,故在Rt⊿CQD中,∠CDQ= arcsin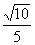 。注:射影“悬空”求线面角的“革命”性意义在于绕开了求线面角中最困难的一步--确定射影的位置,把问题化归为求点到面的距离;而求点到面的距离可以通过“等积转换”实现,并不需要知道射影的确切位置。
。注:射影“悬空”求线面角的“革命”性意义在于绕开了求线面角中最困难的一步--确定射影的位置,把问题化归为求点到面的距离;而求点到面的距离可以通过“等积转换”实现,并不需要知道射影的确切位置。
方法二:“平移”线段。取AD中点E,连BE,如图3-3,易见:BE∥CD,∴CD与平面ADMN所成的角即BE 与平面ADMN所成的角;不难证明:BN⊥AN,BN⊥AC,∴BN⊥面ADMN,即点B在面ADMN上的射影为N,∠BEN为BE 与平面ADMN所成的角;记BC=a,BN=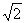 a,BE=
a,BE=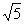 a,在Rt⊿BNE中,∠BEN=arcsin
a,在Rt⊿BNE中,∠BEN=arcsin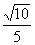 。本题也可以“建系”求,略。
。本题也可以“建系”求,略。
[巩固1]太阳光线斜照地面,地面上与太阳光线成600角的直线有_________条?若太阳光线与地面成60°角时,要使一根长2米的竹竿影子最长,则竹竿与地面所成的角为 。
[巩固2] 在三棱锥P-ABC中,AB⊥BC,AB=BC,PA=2BC,点O是AC的中点,OP⊥底面ABC.求直线PA与平面PBC所成角的大小.
2.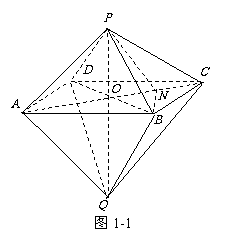 研究异面直线所成的角通常有两种方法。①通过平移使之成为一个平面角,然后解三角形求得;②在空间直角坐标系中利用向量的夹角公式。[注意] 异面直线所成角的范围是:(00,900], 如: cos <
研究异面直线所成的角通常有两种方法。①通过平移使之成为一个平面角,然后解三角形求得;②在空间直角坐标系中利用向量的夹角公式。[注意] 异面直线所成角的范围是:(00,900], 如: cos <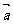 ,
,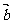 >=-
>=-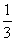 ,则异面直线 a, b所成的角为 arccos
,则异面直线 a, b所成的角为 arccos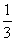 。
。
[举例] 如图, 已知两个正四棱锥
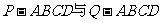 的高分别为1和2,
的高分别为1和2,
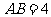 ,(Ⅰ) 证明:
,(Ⅰ) 证明:  ;
;
(Ⅱ) 求异面直线AQ与PB所成的角;
解析:(Ⅰ)记AC、BD交于O,连PO、QO,
则PO⊥面ABCD,QO⊥面ABCD,∴P、Q、O
共线,PQ⊥面ABCD;
(Ⅱ)方法一:“平移”:注意到AC、PQ交于O,
取OC的中点N,连结PN,BN,
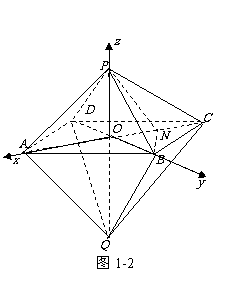 ∵
∵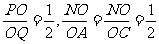 ,∴
,∴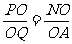 ,故AQ∥PN. ∠BPN是异面直线AQ与PB
,故AQ∥PN. ∠BPN是异面直线AQ与PB
所成的角(或其补角). 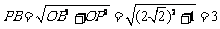
∵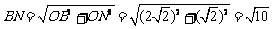
∴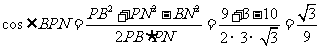
故异面直线AQ与PB所成的角是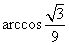 .
.
方法二:“建系”:由题设知,ABCD是正方形,
∴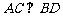 .由(I),
.由(I),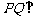 平面
平面 ,故
,故
可以分别以直线CA、DB、QP为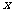 轴,
轴,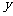 轴,
轴,
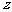 轴建立空间直角坐标系(如图1-2),由题设,
轴建立空间直角坐标系(如图1-2),由题设,
相关各点的坐标分别是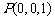 ,
,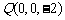 ,
,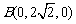 ,
,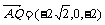 ,
,
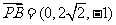 ,于是
,于是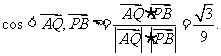
注:在“平移”时常用到一些平面图形的性质,如:三角形的中位线、梯形中位线、平行四边形、平行线分线段成比例定理的逆定理甚至三角形相似等。
[巩固1]异面直线 a, b所成的角为600,则过空间中一点P与a, b都成300的直线有几条?与a, b都成500的直线有几条?与a, b都成600的直线有几条?与a, b都成700的直线有几条?[变形]过大小为600的二面角外一点P作与它的两个面都成600的直线有几条?
 [巩固2
]设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
[巩固2
]设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com