2．为适应城市发展，该城市在2001年调整了距市中心3-5 km范围内的主要用地性质。其调整方案最可能是　　 　 　　　　　　　　　　　　　　　　　　　 (　　 )

A．居住用地调整为商业用地　　 　　　　　　 B．商业用地调整为工业用地

C．工业用地调整为居住用地　 　　　　　　 D．居住用地调整为工业用地

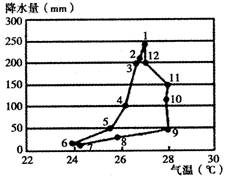读“某地多年平均月降水量及月均温分布图”，回答3-4题。

1．该城市在距市中心0-1 km范围内建筑物的平均高度最高，其原因主要是 (　　 )

A．交通通达度最高　 　　　　　　　　　　　　　　 B．降低单位建筑面积的土地成本

C．居住的人口最多　　 　　　　　　　　　　　　 D．城市的政治服务职能高度集中

2010.3

本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。全卷共300分。考试用时150分钟。

第Ⅰ卷(选择题，共140分)

本卷共35小题，每小题4分，共140分。在每小题给出的四个选项中，只有一项是符合题目要求的。

城市建筑的密度与高度受多种因素的影响。下表为某城市1992年和2008年距市中心不同距离建筑物的平均高度表(单位：米)，回答1-2题。

22．(本小题满分12分)

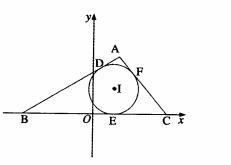
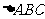的内切圆与三边AB、BC、CA的切点分别为D、E、F，已知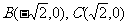，内切圆圆心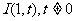，设点A的轨迹为L。

(1)求L的方程；

(2)过点C的动直线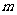交曲线L于不同的两点M、N，问在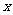轴上是否存在一定点Q(Q不与C重合)，使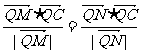恒成立，若存在，试求出Q点的坐标，若不存在，说明理由。

21．(本小题满分12分)

设函数

(1)若函数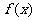在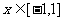内没有极值点，求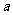的取值范围。

(2)若对任意的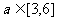，不等式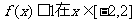上恒成立，求实数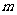的取值范围。

20．(本小题满分12分)

数列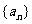中，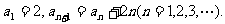

(1)求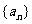的通项公式；

(2)设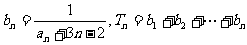，求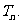

19．(本小题满分12分)

如图所示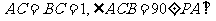，平面ABC，CE//PA，PA=2CE=2。

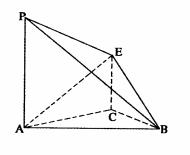(1)求证：平面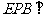平面APB；

(2)求二面角A-BE-P的正弦值。

18．(本小题满分12分)

袋中有分别写着“团团”和“圆圆”的两种玩具共7个，且形状完全相同，从中任取2个玩具都是“圆圆”的概率为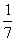，A、B两人不放回从袋中轮流摸取一个玩具，A先取，B后取，然后A再取，……直到两人中有一人取到“圆圆”时即停止游戏，每个玩具在每一次被取出的机会是均等的，用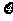表示游戏终止时取玩具的次数。

(1)求袋中“圆圆”的个数；

(2)求3的概率。

17．(本小题满分10分)

已知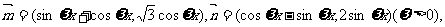若，且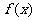的图象相邻的对称轴间的距离等于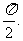

(1)求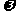的值；

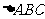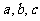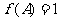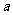(2)在中，分别是角A，B，C的对边，，且，求的最小值。

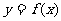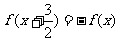16．已知定义在R上的函数满足条件，且函数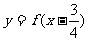是奇函数，给出以下四个命题：

①函数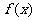是周期函数；

②函数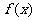的图象关于点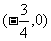对称；

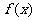③函数是偶函数；

④函数在R上是单调函数。

在上述四个命题中，真命题的序号是　　 (写出所有的真命题的序号)。