
1. 已知集合
已知集合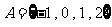 ,
, ,则
,则 .
.
22.(本小题满分14分)设 是函数
是函数 的两个极值点.
的两个极值点.
(Ⅰ)若 ,求函数
,求函数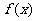 的解析式;
的解析式;
(Ⅱ)若 ,求
,求 的最大值;
的最大值;
(Ⅲ)若 且
且 ,函数
,函数 ,求证
,求证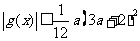 .
.






21.(本小题满分12分)已知椭圆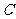 的中心在原点,离心率等于
的中心在原点,离心率等于 ,一条准线方程为
,一条准线方程为 .
.
(Ⅰ)求椭圆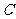 的方程;
的方程;
(Ⅱ)设点 在该椭圆
在该椭圆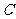 上,
上,  是椭圆
是椭圆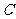 的左右焦点,若
的左右焦点,若 与向量
与向量 共线,求点
共线,求点 的坐标;
的坐标;
(Ⅲ)过椭圆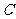 的右焦点
的右焦点 的直线
的直线 交椭圆
交椭圆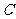 交于
交于 、
、 两点,交
两点,交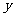 轴于
轴于 点,若
点,若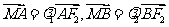 ,求证
,求证 为定值.
为定值.
20. (本小题满分12分)已知首项为负的数列 中,相邻两项不为相反数,且前
中,相邻两项不为相反数,且前 项和为
项和为 .
.
(Ⅰ)证明数列 为等差数列;
为等差数列;
(Ⅱ)设数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 都有
都有 成立,求
成立,求 的最大值.
的最大值.
19.(本小题满分12分)已知直线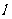 过点
过点 且它的一个方向向量为
且它的一个方向向量为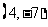 ,又圆
,又圆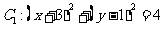 与圆
与圆 关于直线
关于直线 对称。
对称。
(Ⅰ)求直线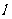 和圆
和圆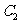 的方程;
的方程;
(Ⅱ)设 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线 和
和 ,它们分别与圆
,它们分别与圆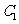 和圆
和圆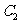 相交,且直线
相交,且直线 被圆
被圆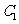 截得的弦长与直线
截得的弦长与直线 被圆
被圆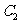 截得的弦长相等,试示所有满足条件的点
截得的弦长相等,试示所有满足条件的点 的坐标.
的坐标.
18.(本小题满分12分)在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的。评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分。某考生有4道题已选对正确答案,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜。
(Ⅰ) 求该考生得40分的概率;
(Ⅱ) 求该考生得不超过30分的概率.
17.(本小题满分12分)已知在 中,角
中,角 、
、 、
、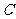 的对边分别是
的对边分别是 、
、 、
、 ,且
,且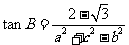 ,
, 。
。
(Ⅰ) 求 的值;
的值;
(Ⅱ) 求 的值.
的值.
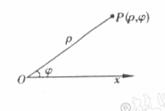
16.在平面上取定一点 ,从
,从 出发引一条射线
出发引一条射线 ,再取定一个长度单位及计算角的正方向,合称为一个极坐标系。这样,平面上任一点
,再取定一个长度单位及计算角的正方向,合称为一个极坐标系。这样,平面上任一点 的位置就可以用线段
的位置就可以用线段 的长度
的长度 以及从
以及从 到
到 的角度
的角度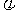 来确定,有序数对
来确定,有序数对 称为
称为 点的极坐标,
点的极坐标, 称为
称为 点的极径,
点的极径,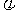 称为
称为 点的极角。在一个极坐标系下,给出下列命题:
点的极角。在一个极坐标系下,给出下列命题:
①点 的极径为4,极角为
的极径为4,极角为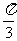 ;
;
②有序数对 与
与 表示两个不同点;
表示两个不同点;
③过点 垂直极轴的直线方程为
垂直极轴的直线方程为 ;
;
④圆心在 ,半径
,半径 的圆的极坐标方程为
的圆的极坐标方程为 。
。
其中真命题序号是
. 
15.如图,过抛物线 的焦点的直线依次交抛物线与圆
的焦点的直线依次交抛物线与圆 于
于 ,则
,则 .
.
14.
 的展开式中的常数项是 .
的展开式中的常数项是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com