
20.(本小题满分16分)
设函数 ,
, .
.
(Ⅰ)若 ,求
,求 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数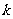 和
和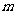 ,使得
,使得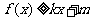 和
和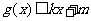 ?若存在,求出
?若存在,求出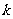 和
和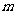 的值.若不存在,说明理由.
的值.若不存在,说明理由.
(Ⅲ)设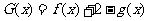 有两个零点
有两个零点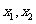 ,且
,且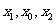 成等差数列,试探究
成等差数列,试探究 值的符号.
值的符号.
盐城市2009/2010学年度高三年级第二次调研考试
数学附加题部分
(本部分满分40分,考试时间30分钟)
19.(本小题满分16分)
设等比数列 的首项为
的首项为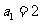 ,公比为
,公比为 (
( 为正整数),且满足
为正整数),且满足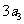 是
是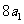 与
与 的等差中项;数列
的等差中项;数列 满足
满足 (
(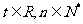 ).
).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)试确定 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(Ⅲ)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数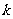 ,在
,在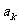 与
与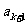 之间插入
之间插入 个2,得到一个新数列
个2,得到一个新数列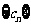 . 设
. 设 是数列
是数列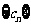 的前
的前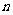 项和,试求满足
项和,试求满足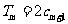 的所有正整数
的所有正整数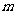 .
.
18.(本小题满分16分)
已知在△ 中,点
中,点 、
、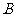 的坐标分别为
的坐标分别为 和
和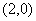 ,点
,点 在
在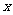 轴上方.
轴上方.
(Ⅰ)若点 的坐标为
的坐标为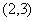 ,求以
,求以 、
、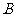 为焦点且经过点
为焦点且经过点 的椭圆的方程;
的椭圆的方程;
(Ⅱ)若∠ ,求△
,求△ 的外接圆的方程;
的外接圆的方程;
(Ⅲ)若在给定直线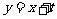 上任取一点
上任取一点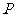 ,从点
,从点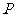 向(Ⅱ)中圆引一条切线,切点为
向(Ⅱ)中圆引一条切线,切点为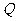 . 问是否存在一个定点
. 问是否存在一个定点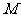 ,恒有
,恒有 ?请说明理由.
?请说明理由.
17.(本小题满分14分)
 如图,互相垂直的两条公路
如图,互相垂直的两条公路 、
、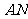 旁有一矩形花园
旁有一矩形花园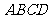 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园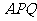 ,要求
,要求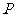 在射线
在射线 上,
上,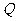 在射线
在射线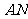 上,且
上,且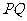 过点
过点 ,其中
,其中 米,
米,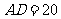 米. 记三角形花园
米. 记三角形花园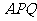 的面积为S.
的面积为S.

 (Ⅰ)当
(Ⅰ)当 的长度是多少时,S最小?并求S的最小值.
的长度是多少时,S最小?并求S的最小值.
 (Ⅱ)要使S不小于
(Ⅱ)要使S不小于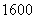 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?





16.(本小题满分14分) w ww.ks 5u.c o
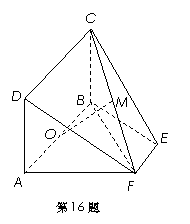 如图,等腰梯形
如图,等腰梯形 中,
中, ,
,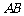 =2,
=2, ,
,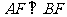 ,
, 为
为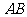 的中点,矩形
的中点,矩形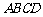 所在的平面和平面
所在的平面和平面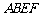 互相垂直.
互相垂直.
(Ⅰ)求证: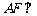 平面
平面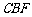 ;
;
(Ⅱ)设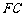 的中点为
的中点为 ,求证:
,求证: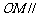 平面
平面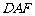 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
15.(本小题满分14分)
在△ 中,角
中,角 、
、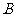 、
、 所对的边分别为
所对的边分别为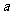 、
、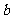 、
、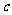 ,且
,且 .
.
(Ⅰ)若 ,求角
,求角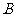 ;
;
(Ⅱ)设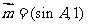 ,
,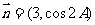 ,试求
,试求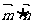 的最大值.
的最大值.
14.设函数 ,则下列命题中正确命题的序号有 ▲ . (请将你认为正确命题的序号都填上)
,则下列命题中正确命题的序号有 ▲ . (请将你认为正确命题的序号都填上)
①当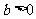 时,函数
时,函数 在R上是单调增函数; ②当
在R上是单调增函数; ②当 时,函数
时,函数 在R上有最小值;
在R上有最小值;
③函数 的图象关于点
的图象关于点 对称;
④方程
对称;
④方程 可能有三个实数根.
可能有三个实数根.
13.若二次函数 的值域为
的值域为 ,则
,则 的最小值为 ▲ .
的最小值为 ▲ .
12.设等差数列 的首项及公差均是正整数,前
的首项及公差均是正整数,前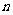 项和为
项和为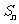 ,且
,且 ,
,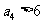 ,
, ,则
,则
= ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com