
(17)(本小题满分12分)
海岛B上有一座为10米的塔,塔顶的一个观测站A,上午11时测得一游船位于岛北偏东15°方向上,且俯角为30°的C处,一分钟后测得该游船位于岛北偏西75°方向上,且俯角45°的D处。(假设游船匀速行驶)
(I) 求该船行使的速度(单位:米/分钟)
(II) 又经过一段时间后,油船到达海岛B的正西方向E处,问此时游船距离海岛B多远。

18.(本小题满分12分)
甲、乙两位学生参加数学竞赛培训,现分别从他们的培训期间参加的若干次预赛成中随机抽取8次,记录如下
甲:82,91,79,78,95,88,83,84
乙:92,95,80,75,83,80,90,85
(I) 画出甲、乙两位学生成绩的茎叶图;
(II) 现要从中选派一人参加数学竞赛,从统计学角度,你认为派哪位学生参加合请说明理由。
(III)
若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为 ,求
,求 的分布列及数学期望E
的分布列及数学期望E
(19)(本小题满分12分)
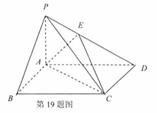 四棱锥
四棱锥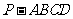 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,
, ,且
,且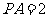 ,点
,点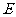 满足
满足
(I)
求证: 平面ABCD;
平面ABCD;
(II)
求二面角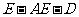 的余弦值。
的余弦值。
(20)(本小题满分12分)
已知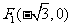 ,
,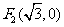 ,动点P满足
,动点P满足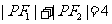 ,记动点P的轨迹为E。
,记动点P的轨迹为E。
(I) 求E的方程。
(II)
曲线E的一条切线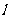 ,过
,过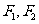 作
作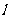 发的垂线,垂足分别为M,N,求
发的垂线,垂足分别为M,N,求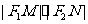 的值。
的值。
(III)
曲线E的一条切线为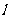 ,与
,与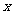 轴,
轴,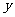 分别交于A,B两点,求
分别交于A,B两点,求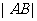 的最小值,并求此时切线的斜率。
的最小值,并求此时切线的斜率。
(21)(本小题满分12分)
已知
(I)
求 的单调区间;
的单调区间;
(II)
当 时,求
时,求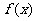 在定义域上的最大值;
在定义域上的最大值;
(III)
求证:
请考生在(22)(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目对应题号涂黑。
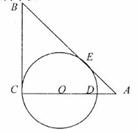
(22)(本小题满分10分)选修4-1;几何证明选讲
已知 中,
中, 是AC上一点,以O为圆心,OC为半径的圆交AC于D,与AB切于E,若AD=2,AE=4,求BE的长。
是AC上一点,以O为圆心,OC为半径的圆交AC于D,与AB切于E,若AD=2,AE=4,求BE的长。
(23)(本小题满分10分)选修4-4,坐标系与参数方程
曲线 极坐标方程为
极坐标方程为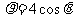 ,直线
,直线 参数方程为
参数方程为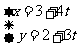 (
(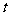 为参数)
为参数)
(I)
将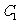 化为直角坐标方程。
化为直角坐标方程。
(II)
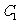 与
与 是否相交?若相交求出弦长,不相交说明理由。
是否相交?若相交求出弦长,不相交说明理由。
(24)(本小题满分10分)选修4-5;不等式选讲
设函数 +
+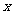
(I)
求函数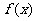 的值域;
的值域;
(II)
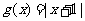 ,求
,求 成立时的
成立时的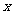 的取值范围。
的取值范围。
(13)抛物线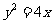 上的点M到其焦点F的距离为4,则点M的横坐标是
。
上的点M到其焦点F的距离为4,则点M的横坐标是
。
(14)已知某空间几何体的正视图、侧视图、俯视图都是等腰直角三角形,且直角边长为1,试写满足以上条件的一个几何体的表面积 。
(15)已知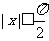 ,
,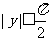 ,其中满足:“
,其中满足:“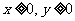 ,且
,且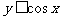 ”的概率为
”的概率为
。
(16)给出下列四个命题:
①如果命题“ ”与命题“
”与命题“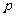 或
或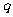 ”都是真命题,那么命题
”都是真命题,那么命题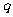 一定是真命题
一定是真命题
②命题“若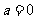 ,则
,则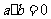 ”的否命题是:“若
”的否命题是:“若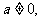 则
则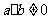 ”
”
③“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
④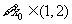 ,使得
,使得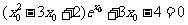 成立
成立
其中正确命题的序号为 。
(1)已知集合 ,
,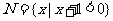 ,则
,则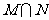 =
=
A.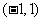 B.
B.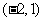
C.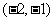 D.
D.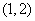
(2)复数 的实部与虚部之和为
的实部与虚部之和为
A. B.0 C.1 D.2
B.0 C.1 D.2
(3)已知平面向量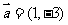 ,
, ,若
,若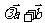 与
与 垂直,则
垂直,则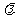 的值
的值
A.-2 B.1 C.-1 D.2
(4)已知公差不为零的等差数列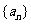 ,若
,若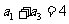 ,且
,且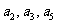 成等比数列,则其前
成等比数列,则其前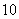 项和
项和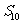 为
为
A.90 B.100 C.110 D.120
(5)身穿红、黄两种颜色衣服的各有两人,现将这4人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )种
A.4 B.6 C.8 D.16
(6)将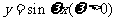 的图像向左平移
的图像向左平移 个单位,平移后的图像如图所示,则平移后的图像所对应的函数解析式是
个单位,平移后的图像如图所示,则平移后的图像所对应的函数解析式是
A.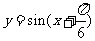 B.
B.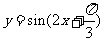
C.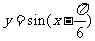 D.
D.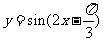

(7)双曲线方程为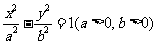 ,过右焦点F向一条渐近线做垂线,垂足为M,如图所示,已知
,过右焦点F向一条渐近线做垂线,垂足为M,如图所示,已知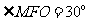 (O为坐标原点),则其离心率为
(O为坐标原点),则其离心率为
A.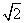 B.
B. C.
C. D.2
D.2
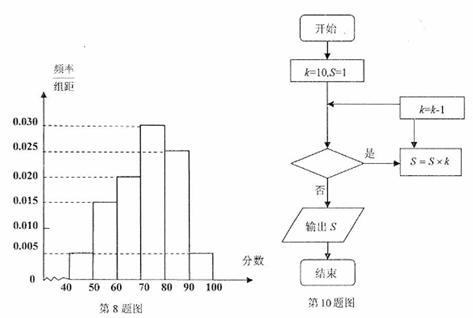
(8)某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数分别是
A.73.3 75 B.73.3,80 C.70,70 D.70,75
(9)已知实数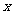 、
、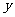 满足
满足 ,则目标函数
,则目标函数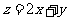 的最大值为
的最大值为
A.12 B.11 C.10 D.3
(10)如图所示的程序框图,若输出的结果为 ,那么判断框中可以填入的关于
,那么判断框中可以填入的关于 的条件是
的条件是
A.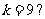 B.
B.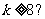 C.
C.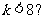 D.
D.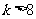
(11))设A为空间一点, 是两条直线,
是两条直线, 是两个平面,有下列四个命题:
是两个平面,有下列四个命题:
① 了,则
了,则 可能为异面直线。
可能为异面直线。
②若 则
则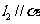
③已知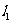 与
与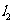 为异面直线,
为异面直线,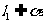 ,
, ,则
,则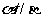
④若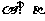 ,
,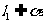 ,则
,则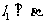
其中正确命题的序号是
A.①③ B.②④ C.②③ D.①④
(12)设 在
在 上有定义,对于给定的诗书K,定义函数
上有定义,对于给定的诗书K,定义函数
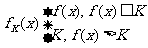 ,给出函数
,给出函数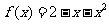 ,若对于任意
,若对于任意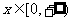 ,恒有
,恒有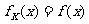 ,则
,则
A.K的最大值为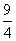 B.K的最小值为
B.K的最小值为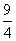
C.K的最大值为2 D.K的最小值为2
第II卷
本卷包括必考题和选考题两部分。第(13)题~第(21)题为必考题,每个试题考生都必须作答。第(22)题~(24)题为选考题,考生根据要求做答。
(17)(本小题满分12分)
如图,已知 ,点O为坐标原点,点B在第二象限,且
,点O为坐标原点,点B在第二象限,且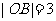 ,记
,记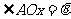 。
。
(I)
 求
求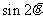 。
。
(II)
若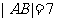 ,求
,求 的值
的值
(18)(本小题满分12分)
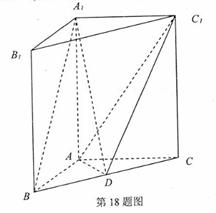 在直三棱柱
在直三棱柱 中,
中,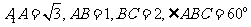 ,D是BC的中点。
,D是BC的中点。
(I)
求证: 平面
平面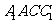 ;
;
(II)
求证: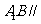 平面
平面 ;
;
(III)
求三棱锥 的体积。
的体积。
(19)(本小题满分12分)
下表为某学年随机抽出的100名学生的数学及语文成绩,成绩分为1~5个档次,设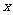 、
、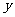 分别表示数学成绩和语文成绩,例如表中数学成绩为5分的共有
分别表示数学成绩和语文成绩,例如表中数学成绩为5分的共有 ,语文成绩2分的共有
,语文成绩2分的共有 人。
人。

(I)
求 的概率及
的概率及 且
且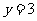 的概率;
的概率;
(II)
求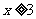 的概率及在
的概率及在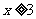 的基础上,
的基础上,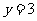 的概率;
的概率;
(III)
求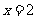 的概率及
的概率及 的值。
的值。
(20)(本小题满分12分)
已知函数
(I)
求 的单调区间;
的单调区间;
(II)
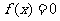 在
在 上有解,求
上有解,求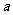 的取值范围。
的取值范围。
(21)(本小题满分12分)
已知 ,动点P满足
,动点P满足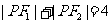 ,记动点P的轨迹为E
,记动点P的轨迹为E
(I) 求E的方程;
(II)
曲线E的一条切线为 ,过
,过 作
作 的垂线,垂足分别为M,N,求
的垂线,垂足分别为M,N,求 的值;
的值;
(III)
曲线E的一条切线为 ,与
,与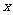 轴分别交于A,B两点,求
轴分别交于A,B两点,求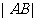 的最小值,并求此时切线的斜率。
的最小值,并求此时切线的斜率。
请考生在(22)(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目对应题号涂黑。
(22)(本小题满分10分)选修4-1;几何证明选讲
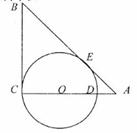
已知 中,
中, 是AC上一点,以O为圆心,OC为半径的圆交AC于D,与AB切于E,若AD=2,AE=4,求BE的长。
是AC上一点,以O为圆心,OC为半径的圆交AC于D,与AB切于E,若AD=2,AE=4,求BE的长。
(23)(本小题满分10分)选修4-4,坐标系与参数方程
曲线 极坐标方程为
极坐标方程为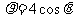 ,直线
,直线 参数方程为
参数方程为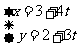 (
( 为参数)
为参数)
(I)
将 化为直角坐标方程。
化为直角坐标方程。
(II)
 与
与 是否相交?若相交求出弦长,不相交说明理由。
是否相交?若相交求出弦长,不相交说明理由。
(24)(本小题满分10分)选修4-5;不等式选讲
设函数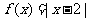 +
+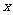
(I)
求函数 的值域;
的值域;
(II)
 ,求
,求 成立时的
成立时的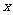 的取值范围。
的取值范围。
(13)在等比数列 中,已知
中,已知 ,前三项和
,前三项和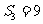 ,则公比
,则公比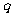 的值为 。
的值为 。
(14)一个多面体的三是图如图所示,它的标面积为 。

(15)设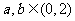 ,则关于
,则关于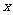 的方程
的方程 在
在 上有两个不等的实根的概率为
。
上有两个不等的实根的概率为
。
(16)下列说法正确的是
①“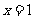 ”是“
”是“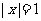 ”的充分不必要条件
”的充分不必要条件
②若命题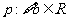 ,使
,使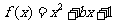 是偶函数,则
是偶函数,则
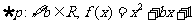 都不是偶函数
都不是偶函数
③命题“若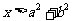 ,则
,则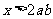 ”的逆命题为真命题。
”的逆命题为真命题。
④因为指数函数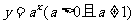 是增函数(大前提),而
是增函数(大前提),而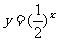 是指数函数(小前提),所以
是指数函数(小前提),所以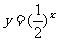 是增函数(结论),此推理的结论错误的原因是大前提错误。
是增函数(结论),此推理的结论错误的原因是大前提错误。
(1)已知集合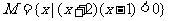 ,
, ,则
,则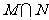 =
=
A.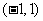 B.
B.
C.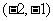 D.
D.
(2)复数 的实部与虚部之和为
的实部与虚部之和为
A. B.0 C.1 D.2
B.0 C.1 D.2
(3)函数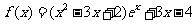 ,则存在函数零点的区间是
,则存在函数零点的区间是
A. B.
B.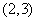 C.
C.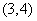 D.
D.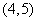
(4)若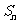 是等差数列
是等差数列 的前
的前 项和,且
项和,且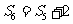 ,则
,则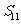 的值为
的值为
A.12 B.18 C.22 D.44
(5) 中,
中,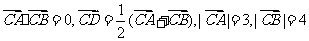 ,则向量
,则向量 与
与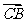 夹角的余弦值为
夹角的余弦值为
A.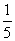 B.
B.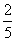 C.
C.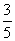 D.
D.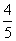
(6)某校从高一年级期末考试的学生中抽出60名学生,统计其成绩(均为整数)的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数分别是
A.73.3 75 B.73.3,80 C.70,70 D.70,75
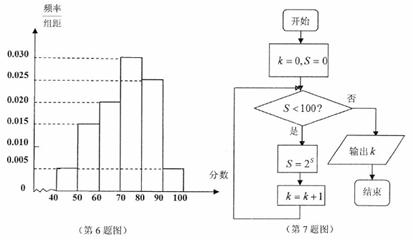
(7)如图所示的程序框图运行后输出的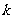 的值是
的值是
A.4 B.5 C.7 D.8
(8)若圆M与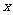 轴负半轴相切,与
轴负半轴相切,与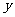 轴相交于点(0,2),(0,8),则圆心M的坐标为
轴相交于点(0,2),(0,8),则圆心M的坐标为
A.(-5,3) B.(5,4) C.(3,5) D.(-4,5)
(9)某地一天从6~14时的温度变化曲线近似满足函数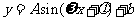 ,则这段曲线得函数解析式为
,则这段曲线得函数解析式为
A.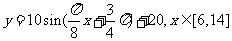
B.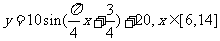
C.
D.
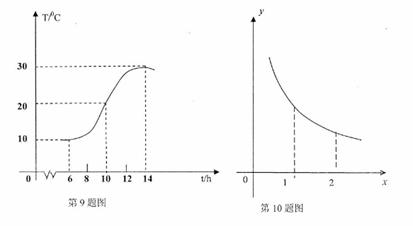
10.已知函数 在区间
在区间 上的图像如图所示,记为
上的图像如图所示,记为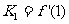 ,
,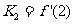 ,
,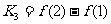 ,则
,则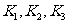 之间的大小关系为
之间的大小关系为
A. B.
B.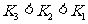
C. D.
D.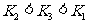
(11)设A为空间一点, 是两条直线,
是两条直线,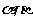 是两个平面,有下列四个命题:
是两个平面,有下列四个命题:
① 了,则
了,则 可能为异面直线。
可能为异面直线。
②若 则
则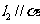
③已知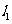 与
与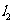 为异面直线,
为异面直线,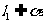 ,
,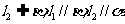 ,则
,则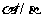
④若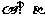 ,
,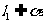 ,则
,则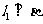
其中正确命题的序号是
A.①③ B.②④ C.②③ D.①④
(12)设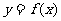 在
在 上有定义,对于给定的诗书K,定义函数
上有定义,对于给定的诗书K,定义函数
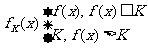 ,给出函数
,给出函数 ,若对于任意
,若对于任意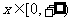 ,恒有
,恒有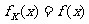 ,则
,则
A.K的最大值为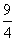 B.K的最小值为
B.K的最小值为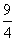
C.K的最大值为2 D.K的最小值为2
第II卷
本卷包括必考题和选考题两部分。第(13)题~第(21)题为必考题,每个试题考生都必须作答。第(22)题~(24)题为选考题,考生根据要求做答。
17.下面是2010年广州亚运会吉祥物--乐羊羊的标示,请你以设计者的身份说明吉祥物标示的创意。要求说明内容准确,语意简明,句子通顺,不超过120个字。(5分)

16.下面一则文稿在表达上有三处不妥当,请指出并改正。(6分)
通告
为提高电话网的通讯能力,我公司将对辖区电话局的交换机进行升级改造,现依据《中年人民共和国电信条例》,将有关事项宣布如下:本工程将于2009年11月12日20时至13日8时施工,在此期间会影响青山区电话用户的正常通话。交换机升级后,用户原有的一些业务功能(如闹钟、呼叫转移等)需要重新设置;热线和呼出限制的设置方法也有变化。
如有疑问,欢迎提出。本公司客服电话:87654321。
对工程施工给您造成的不便.我们深表不安。请予理解和支持。
天网通信有限公司青山分公司
2009年11月2日
(1) 改
(2) 改
(3) 改
15.依次填入下面一段文字横线处的语句,衔接最恰当的一组是(3分) ( )
评论者在解析艺术技巧时,一定要把从作品的整体构造入手和从作品的构成要素入手这两个方面结合起来。 这样才能取得坚实、明白的效果。
①容易写得空洞、枯涩、难琢磨; ②又容易支离破碎、只顾一点,不及其余。
③最好是从大处着眼, ④有宏观的综述, ⑤如果只是从细微处去解析, ⑥从细微处人手, ⑦如果只是从整体着眼, ⑧也有具体的分析。
A.③④⑥⑧⑦①⑤② B.⑦①⑤②③⑥④⑧
C.③⑥④⑧⑤①⑦② D.⑤①⑦②③④⑥⑧
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com