2.文中运用了大量的古代神话传说，这样写有什么作用?

1.曾国藩为什么要把自己的住所题作“求阙斋”?

2．巧引名言(警句)添文采。托尔斯泰说应多用“金刚钻的语言”进行写作。警句名言就无疑是一种“金刚钻”。

如无锡市一考生的《精彩语文》一文中有这样一段：

伴着你，陶渊明的朵朵菊花点缀了朦胧的南山，龚自珍的片片落红幻化成软软的春泥，晏殊的独自徘徊落寞了通幽曲径，温庭筠的脉脉斜晖笼罩了悠悠的碧水……

如江苏盐城一考生写的《语文从我身边轻轻走过》则运用了联用古诗名句的妙招：

如果你是“大漠孤烟直，长河落日圆”的边塞大漠，我愿飞奔在漫天黄沙里；如果你是“惊涛拍岸，卷起千堆雪”的浩淼长江，我愿遨游于猛浪湍流中；如果你是“山重水复疑无路，柳暗花明又一村”的深山丛林，我愿跋涉在荆棘小道上。啊，语文，美丽如你，叫我爱不释手。

如江苏考生《西安与南京：山与水的对话》

南京，长江南岸的明珠，是苏浙纵横交错的河流湖泊给了明珠最灵动的光泽。抬眼望，“秦淮水榭花开早”，回首瞧，“燕子飞时，绿水人家绕”。那里的“六朝旧事如流水”，那里的“夜船吹笛雨潇潇”。南京用那上天赋予的水，勾勒出如梦如幻、如诗如画的“好江南”。……西安无言，南京无言，一个背靠秦岭，一个脚踏长江，却一起“面朝大海”，霎时“春暖花开”。

此段文字妙在扣合题意而又能充分激活自己的诸多文化积淀，文章显得充实而又灵动，哲理与诗情、历史与现实，融为一体，信手拈来的诗文名句，不露斧凿之痕，结尾化用海子的名句，尤为贴切自然，并赋予了新的意蕴。

1．巧借熟语显睿智。“正确使用熟语”是2004年以来高考新增的考点，它包含成语、俗语、谚语、格言、歇后语等，报刊上巧用熟语的，仅是文章标题就很多，如《考试马拉松要不得》、《有心栽花花更发》、《人情消费，温柔一刀》等等。如能在文中恰当使用，可化平淡为神奇，起到锦上添花之效。如：

古人说：“上有天堂，下有苏杭。”古往今来，美丽的西湖承载了多少中国文人的梦幻？苏轼虽被贬至此，然而他没有悲怆，没有怨天尤人，既来之，则安之，一蓑烟雨任平生。他懂得了“为官一任，造福一方”、“当官不为民做主，不如回家卖红薯”的简单道理。于是，一道苏堤便横卧西湖，他要让西湖储藏的心灵，淹没他所有的痛苦、所有的忧伤。(福建考生《苏轼的赤壁》)

“怨天尤人”“既来之，则安之”“当官不为民做主，不如回家卖红薯”等熟语的使用使得文章语言清新灵动，熠熠生辉，意蕴平添。

22．(本小题满分12分)

已知椭圆方程为，它的一个顶点为，离心率．

(1)求椭圆的方程；

(2)设直线l与椭圆交于A，B两点，坐标原点O到直线l的距离为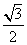，求△AOB面积的最大值．

2010年梧州市高三毕业班第一次测试

21．(本小题满分12分)

已知函数 ，其中R．

(1)若曲线在点处的切线方程为，求函数的解析式；

(2)当时，讨论函数的单调性．

20．(本小题满分12分)

如图，四棱锥的底面是矩形，底面，P为BC边的中点，SB与平面ABCD所成的角为45°，且AD=2，SA=1．

(1)求证：平面SAP;

(2)求二面角A－SD－P的大小.

19．(本小题满分12分)

在数列中，已知a₁=2，a_n+1=4a_n－3n+1，n∈.

(1)设，求证：数列是等比数列;

(2)求数列的前n项和S_n ．

18．(本小题满分12分)

某社区举办2010年上海世博会知识宣传活动，进行现场抽奖，抽奖规则是：盒中装有10张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案，参加者每次从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖．

(1)活动开始后，一位参加者问：盒中有几张“海宝”卡？主持人笑说：我只知道若从盒中抽两张都不是“海宝”卡的概率是，求抽奖者获奖的概率；

(2)现有甲乙丙丁四人依次抽奖，抽后放回，另一个人再抽，求至少有两人获奖的概率.