
20.解:(1)设所求直线方程为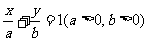
则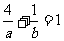

当且仅当 且
且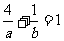 ,即
,即 时取等号
时取等号
故所求直线方程为:
(2)设 ,
,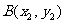 ,则
,则

∴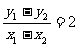
故所求直线方程为:
(21)
解:(1) 直线ED1在平面ABB1A1
上的射影为直线BA1
直线ED1在平面ABB1A1
上的射影为直线BA1
 即: 异面直线ED1与B1A所成的角为
即: 异面直线ED1与B1A所成的角为
(2)若CF
= FD,在正方形ABCD中有 ,
,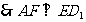
由(1)知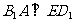 ,
,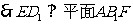 ,
,
故当  时,能使ED1⊥平面AB
时,能使ED1⊥平面AB

解: 
(1)
(2)
得:
(3)设 得:
得:
 ,
,
所以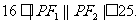

(1)
(2)
得:
(3)设 得:
得:
 ,
,
所以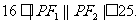
22.(本小题12分)
P为椭圆 上一点,左、右焦点分别为F1,F2。
上一点,左、右焦点分别为F1,F2。
(1)若PF1的中点为M,求证|MO|= |PF1|;
|PF1|;
(2)若∠F1PF2=60°,求|PF1||PF2|之值。
(3)求|PF1||PF2|的最值。
第Ⅰ卷选择题
|
1、▄ [B] [C] [D] 4、▄ [B] [C] [D] 7、▄ [B] [C] [D] 10、[A] ▄ [C] [D] 2、[A] ▄ [C] [D] 5、[A] [B] ▄ [D] 8、[A] [B] ▄ [D] 11、[A] [B] [C] ▄ 3、[A] [B] [C] ▄ 6、▄ [B] [C] [D] 9、[A] ▄[C] [D] 12、[A] [B] ▄ [D] ▄ |
第Ⅱ卷 非选择题
|
二、填空题 (13) 相离 (14)  (15) (0.5,2) (16) (-2,-1) 请在各题目的答题区域内作答,超出黑色矩形框限定区域的答案无效 |
|
三、解答题 (17) 证明:因为  、 、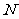 分别为 分别为 、 、 的中点。 的中点。所以MN平行于 BD 又因为BD不在平面AMN内,MN在平面AMN内 所以  面 面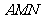 ; ; |
(18)解:
解:设所求双曲线方程为:
双曲线过点M , 得 双曲线方程为
双曲线方程为
(19)
解:
(Ⅰ) 要使圆的面积最小,则AB为圆的直径,
∴所求圆的方程为(x-2)(x+2)+(y+3)(y+5)=0,即
x2+(y+4)2=5.····················································································· 5分
(Ⅱ) 因为kAB=12,AB中点为(0,-4),
所以AB中垂线方程为y+4=-2x,即2x+y+4=0.····························· 8分
解方程组 得
得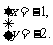 即圆心为(-1,-2).
即圆心为(-1,-2).
根据两点间的距离公式,得半径r=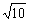 ,
,
因此,所求的圆的方程为(x+1)2+(y+2)2=10.····································· 12分
另解:设所求圆的方程为(x-a)2+(y-b)2=r2,根据已知条件得



所以所求圆的方程为(x+1)2+(y+2)2=10.
21.(本题12分)
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是CD上
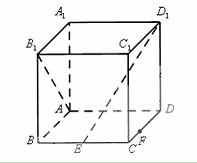 的动点.
的动点.
(1)求异面直线ED1与B1A所成角的大小;
(2)当 的值为多少时,能使E D1⊥平面AB1F 。
的值为多少时,能使E D1⊥平面AB1F 。
20.(本小题12分)
分别求满足下列条件的直线方程。
(1)过点P(4,1),使它在两坐标轴上截距为正值,且它们的和最小。
(2)与椭圆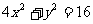 交于A,B两点,且AB中点为
交于A,B两点,且AB中点为 。
。
17(本题10分).如图,在四棱锥 中,
中,  、
、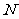 分别
分别
 为
为 、
、 的中点。
的中点。
求证: 面
面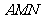 ;
;
18(本题12分)已知双曲线的渐近线的方程是 ,且经过点
,且经过点 ,求双曲线的标准方程。
,求双曲线的标准方程。
19.已知圆C经过点A(2,-3)和B(-2,-5).
(Ⅰ) 当圆C的面积最小时,求圆C的方程;
(Ⅱ) 若圆C的圆心在直线x-2y-3=0上,求圆C的方程.
16.若双曲线 的焦点在y轴上,则m的取值范围是
。
的焦点在y轴上,则m的取值范围是
。
15.已知抛物线 的焦点为F,
的焦点为F, 是此抛物线内部一点,在抛物线上找一点P使
是此抛物线内部一点,在抛物线上找一点P使 取得最小值时, 点P的坐标是
。
取得最小值时, 点P的坐标是
。
14.在长方体 中,已知
中,已知 ,求异面直线
,求异面直线 与
与 所成角的余弦值为
所成角的余弦值为
13. 两圆x2+y2=3与
两圆x2+y2=3与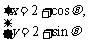 的位置关系是
的位置关系是
12.已知实数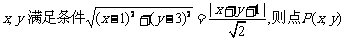 的运动轨迹是( )
的运动轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.圆
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com