
13.补写出下列名篇名句中的空缺部分。 (6分)
吾尝终日而思矣, ; ,不如登高之博见也。
秦人不暇自哀,而后人哀之; , 。
,羡长江之无穷;挟飞仙以遨游, ;知不可乎骤得,托遗响于悲风。
10.下列对原文有关内容的分析和概括,不正确的一项是(3分) ( )
A.齐国进攻鲁国时,鲁国想用吴起做将军,又因吴起娶了齐国女子为妻而猜疑他。
B.魏文侯听说吴起贤明,又很有军事才能,就重用吴起为将军,让他率军进攻秦国, 夺取了五座城池。
C.吴起在楚国担任相职,申明法度,赏罚分明,裁减闲职,废除部分贵族爵位,触犯了王室大臣的利益,最终招致杀身之祸。
D.太史公借俗语“能做的人未必能说,能说的人未必能做”,对吴起的为人作了一个比较客观的评价。
第Ⅱ卷(非选择题,共120分)
9.下列各组句子中,分别表明吴起“善于打战”和“残暴无义”是(3分) ( )
A.将而攻齐,大破之 遂杀其妻,以明不与齐也
B.卧不设席,行不骑乘 捐不急之官,废公族疏远者
C.魏文侯以为将,击秦,拔五城 吴起惧得罪,遂去,即之楚
D.然用兵,司马穰苴不能过也 吴起于是闻魏文侯贤,欲事之
吴起者,卫人也,好用兵。齐人攻鲁,鲁欲将吴起,吴起取齐女为妻,而鲁疑之。吴起于是欲就名,遂杀其妻,以明不与齐也。鲁卒以为将。将而攻齐,大破之。鲁人或恶吴起曰:“起之为人,猜忍人也。其少时,乡党笑之,吴起杀其谤己者三十余人。鲁君疑之,起杀妻以求将。夫鲁小国,而有战胜之名,则诸侯图鲁矣。且鲁卫兄弟之国也,而君用起,则是弃卫。”鲁君疑之,谢吴起。 吴起于是闻魏文侯贤,欲事之。文侯问李克曰:“吴起何如人哉?”李克曰:“起贪而好色,然用兵,司马穰苴不能过也。”于是魏文侯以为将,击秦,拔五城。起之为将,卧不设席,行不骑乘,与士卒分劳苦。文侯以吴起善用兵,乃以为西河守,以拒秦、韩。
魏文侯既卒,起事其子武侯。武侯浮西河而下,中流,顾而谓吴起曰:“美哉乎山河之固,此魏国之宝也!”起对曰:“在德不在险。若君不修德,舟中之人尽为敌国也。”武侯曰:“善。”田文既死,公叔为相,尚魏公主,而害吴起,因谓武侯曰:“夫吴起贤人也。臣窃恐起之无留心也。试延以公主,以此卜之。”吴起果辞魏武侯,武侯疑之而弗信也。吴起惧得罪,遂去,即之楚。 楚悼王素闻起贤,至则相楚,明法审令,捐不急之官,废公族疏远者,以抚养战斗之士。要在强兵,破驰说之言纵横者。故楚之贵戚尽欲害吴起。及悼王死,宗室大臣作乱而攻吴起,吴起走之王尸而伏之。击起之徒因射刺吴起,并中悼王。
太史公曰:世俗所称师旅,皆道吴起《兵法》,世多有,故弗论,论其行事所施设者,语曰:“能行之者未必能言,能言之者未必能行。”吴起说武侯以形势不如德,然行之于楚,以刻暴少恩亡其躯。悲夫! (节选自《史记·吴起列传》,有删节)
8.对下列句子中加点词的解释,不正确的一项是(3分) ( )
A.起事其子武侯。 事:侍奉。
B.公叔为相,尚魏公主。 尚:娶公主为妻。
C.吴起惧得罪,遂去,即之楚。 得罪:招人不快。
D.明法审令,捐不急之官。 捐:除去。
(17)(本小题满分12分)
如图,已知 ,点O为坐标原点,点B在第二象限,且
,点O为坐标原点,点B在第二象限,且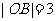 ,记
,记 。
。
(I)
 求
求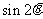 。
。
(II)
若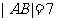 ,求
,求 的值
的值
(18)(本小题满分12分)
 在直三棱柱
在直三棱柱 中,
中, ,D是BC的中点。
,D是BC的中点。
(I)
求证: 平面
平面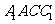 ;
;
(II)
求证: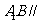 平面
平面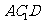 ;
;
(III)
求三棱锥 的体积。
的体积。
(19)(本小题满分12分)
下表为某学年随机抽出的100名学生的数学及语文成绩,成绩分为1~5个档次,设 、
、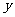 分别表示数学成绩和语文成绩,例如表中数学成绩为5分的共有
分别表示数学成绩和语文成绩,例如表中数学成绩为5分的共有 ,语文成绩2分的共有
,语文成绩2分的共有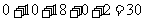 人。
人。

(I)
求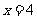 的概率及
的概率及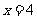 且
且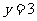 的概率;
的概率;
(II)
求 的概率及在
的概率及在 的基础上,
的基础上,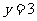 的概率;
的概率;
(III)
求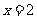 的概率及
的概率及 的值。
的值。
(20)(本小题满分12分)
已知函数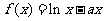
(I)
求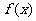 的单调区间;
的单调区间;
(II)
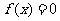 在
在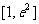 上有解,求
上有解,求 的取值范围。
的取值范围。
(21)(本小题满分12分)
已知 ,动点P满足
,动点P满足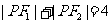 ,记动点P的轨迹为E
,记动点P的轨迹为E
(I) 求E的方程;
(II)
曲线E的一条切线为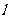 ,过
,过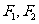 作
作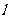 的垂线,垂足分别为M,N,求
的垂线,垂足分别为M,N,求 的值;
的值;
(III)
曲线E的一条切线为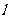 ,与
,与 轴分别交于A,B两点,求
轴分别交于A,B两点,求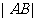 的最小值,并求此时切线的斜率。
的最小值,并求此时切线的斜率。
请考生在(22)(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目对应题号涂黑。
(22)(本小题满分10分)选修4-1;几何证明选讲
已知 中,
中, 是AC上一点,以O为圆心,OC为半径的圆交AC于D,与AB切于E,若AD=2,AE=4,求BE的长。
是AC上一点,以O为圆心,OC为半径的圆交AC于D,与AB切于E,若AD=2,AE=4,求BE的长。

(23)(本小题满分10分)选修4-4,坐标系与参数方程
曲线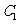 极坐标方程为
极坐标方程为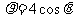 ,直线
,直线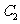 参数方程为
参数方程为 (
(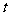 为参数)
为参数)
(I)
将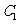 化为直角坐标方程。
化为直角坐标方程。
(II)
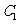 与
与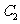 是否相交?若相交求出弦长,不相交说明理由。
是否相交?若相交求出弦长,不相交说明理由。
(24)(本小题满分10分)选修4-5;不等式选讲
设函数 +
+
(I)
求函数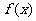 的值域;
的值域;
(II)
 ,求
,求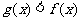 成立时的
成立时的 的取值范围。
的取值范围。
(13)在等比数列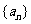 中,已知
中,已知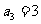 ,前三项和
,前三项和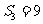 ,则公比
,则公比 的值为 。
的值为 。
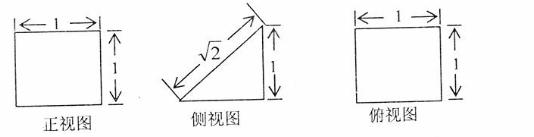
(14)一个多面体的三是图如图所示,它的标面积为 。
(15)设 ,则关于
,则关于 的方程
的方程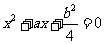 在
在 上有两个不等的实根的概率为
。
上有两个不等的实根的概率为
。
(16)下列说法正确的是
①“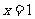 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
②若命题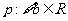 ,使
,使 是偶函数,则
是偶函数,则
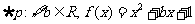 都不是偶函数
都不是偶函数
③命题“若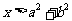 ,则
,则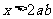 ”的逆命题为真命题。
”的逆命题为真命题。
④因为指数函数 是增函数(大前提),而
是增函数(大前提),而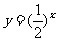 是指数函数(小前提),所以
是指数函数(小前提),所以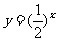 是增函数(结论),此推理的结论错误的原因是大前提错误。
是增函数(结论),此推理的结论错误的原因是大前提错误。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com